936. Cramer’s formula
Solve the system of two
linear equations with two variables using the Kramer's rule. The system of
equations given in the example has the form:
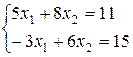
It is known that system has a
unique solution.
Input. The first line contains the
coefficients of the first equation, and the second line contains the
coefficients of the second equation. All numbers are separated with one space
and do not exceed 100 by the absolute value.
Output. Print the first root in the
first line and the second root in the second line with accuracy 0.001.
|
Sample input |
Sample output |
|
5 8
11 -3 6
15 |
-1.000 2.000 |
SOLUTION
algebra – Cramer’s rule
Algorithm analysis
The determinant is a number
equal to
= a * d – b * c
Consider the
system of equations:
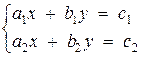
Multiply the
first equation by b2, and
the second by b1:
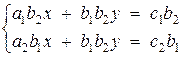
Subtract the
second equation
from the first one:
(a1b2 – a2b1) x = c1b2 – c2b1
Or the same as
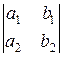x =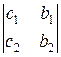 
Similarly, in
the original system, multiply the first equation by a2, and the second by a1:
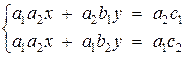
Subtract the
first equation
from the second one:
(a1b2 – a2b1) y = a1c2 – a2c1
Or the same as
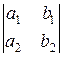y =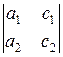 
Let
d = 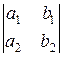, dx = 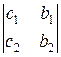, dy =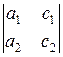
Then the solution to the system of
equations can be written in the form:
x = 
, y = 
, d ¹ 0
Example
Consider the system of equations 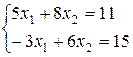. For it we have:
d =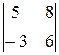 
= 5*6 + 3*8 = 54,
dx =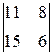 
= 11*6 – 15*8 = -54, dy = 
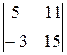= 5*15 + 3*11 = 108,
where from
x = -54 / 54 = -1, y
= 108 / 54 = 2
Algorithm realization
Function kramer solves a system of linear equations by
Cramer's method. The roots of the system are returned in the variables x and y.
int
kramer(double a1, double
b1, double c1,
double a2, double
b2, double c2, double
&x, double &y)
{
double d = a1
* b2 - a2 * b1;
double dx =
c1 * b2 - c2 * b1;
double dy =
a1 * c2 - a2 * c1;
For d = 0,
the lines are parallel.
·
If dx = 0
(and dy = 0), then the
lines coincide, return 2.
·
If dx ≠
0 (in this case dy ≠ 0
also), then the lines do not coincide (do not have common points), return
1.
if (d == 0) return (dx == 0.0) + 1;
For d ≠
0, the system has a unique solution, which is calculated in the pair (x, y).
In this case, we return 0.
x = dx / d; y = dy / d;
return 0;
}
The main part of the program. Read the input data.
scanf("%lf %lf %lf",&a1,&b1,&c1);
scanf("%lf %lf %lf",&a2,&b2,&c2);
Solve the system of equations and print the answer.
kramer(a1,b1,c1,a2,b2,c2,x,y);
printf("%.3lf\n%.3lf\n",x,y);
Java realization
import java.util.*;
public class Main
{
static double[] kramer(double a1, double b1, double c1,
double a2, double b2, double c2)
{
double res[] = new double[3]; // type, x, y
double d = a1 * b2 - a2 * b1;
double dx = c1 * b2 - c2 * b1;
double dy = a1 * c2 - a2 * c1;
if (d == 0)
{
if (dx == dy && dx == 0.0) res[0] = 2;
else res[0] = 1;
}
else
{
res[1] = dx / d;
res[2] = dy / d;
res[0] = 0;
}
return res;
}
public static void
main(String []args)
{
Scanner con = new Scanner(System.in);
double a1 = con.nextDouble();
double b1 = con.nextDouble();
double c1 = con.nextDouble();
double a2 = con.nextDouble();
double b2 = con.nextDouble();
double c2 = con.nextDouble();
double res[] = kramer(a1,b1,c1,a2,b2,c2);
System.out.println(res[1] + "\n" + res[2]);
con.close();
}
}