937. Произведение массива кроме самого себя

Дан массив in из n целых чисел. Постройте массив out такой, чтобы каждый элемент out_i был равен произведению всех элементов массива in, кроме in_i.

Вход. Первая строка содержит целое  число n (1 < n ≤ 10⁶). Вторая строка содержит n целых чисел, каждое по модулю не превышает 100.

Выход. Выведите массив out. Гарантируется, что абсолютное значение каждого выведенного числа не превышает 2 * 10⁹.

Пример входа 1	Пример выхода 1
4 1 2 3 4	24 12 8 6
Пример входа 2	Пример выхода 2
4 2 0 1 4	0 8 0 0

РЕШЕНИЕ

массивы

Анализ алгоритма

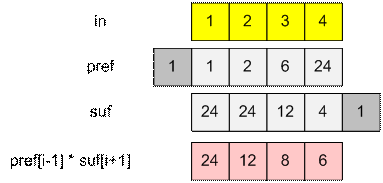
Пусть in – входной массив, индексацию начнем с 1. Тогда входные числа хранятся в in[1], in[2], …, in[n]. Если вычислить произведение p всех элементов массива in, а затем положить out_i = p / in_i (out – результирующий массив), то такой метод не работает в случае, когда in_i = 0.

Рассмотрим другой подход. Построим два массива:

· Массив префиксных произведений pref, в котором

pref[i] = in[1] * in[2] * … * in[i],

при этом положим pref[0] = 1;

· Массив суффиксных произведений suf, в котором

suf[i] = in[i] * in[i + 1] * … * in[n],

при этом положим suf[n + 1] = 1;

Тогда out_i = pref[i – 1] * suf[i + 1].

Пример

Реализация алгоритма

Объявим рабочие массивы.

#define MAX 1000002

int in[MAX], pref[MAX], suf[MAX], res[MAX];

Читаем входные данные.

scanf("%d",&n);

for(i = 1; i <= n; i++)

scanf("%d",&in[i]); // [1,2,3,4]

Строим массив произведений префиксов.

pref[0] = 1;

for(i = 1; i <= n; i++) // [1,2,6,24]

pref[i] = pref[i-1] * in[i];

Строим массив произведений суффиксов.

suf[n+1] = 1;

for(i = n; i >= 1; i--) // [24,24,12,4]

suf[i] = suf[i+1] * in[i];

Строим результирующий массив.

for(i = 1; i <= n; i++) // [24,12,8,6]

res[i] = pref[i-1] * suf[i+1];

Выводим ответ.

for(i = 1; i <= n; i++)

printf("%d ",res[i]);

printf("\n");