937. Product of Array Except Self

Given an array in of n integers. Build an array out such that out_i is equal to the product of all the elements of in except in_i. Solve it in O(n) and constant space complexity.

Input. The first line contains number n (1 < n ≤ 10⁶). The second line contains n integers, each number is not greater than 100 by absolute value.

Output. Print the out array. It is known that all printed values are not greater than 2 *10⁹ by absolute value.

Sample input 1	Sample output 1
4 1 2 3 4	24 12 8 6
Sample input 2	Sample output 2
4 2 0 1 4	0 8 0 0

SOLUTION

arrays

Algorithm analysis

Let in be an input array, its indexing we start from 1. So input data are stored at in[1], in[2], …, in[n]. If one finds the product p of all numbers from array in, and then assigns out_i = p / in_i, such method will not work for the case if in_i = 0.

Consider a different approach. Let’s construct two arrays:

· Array of prefixes pref, where pref[i] = in[1] * in[2] * … * in[i], we also set pref[0] = 1;

· Array of suffixes suf, where suf[i] = in[i] * in[i + 1] * … * in[n], we also set suf[n + 1] = 1;

Then out_i = pref[i – 1] * suf[i + 1].

Sample

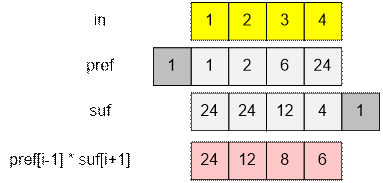
Algorithm realization

Declare working arrays.

#define MAX 1000002

int in[MAX], pref[MAX], suf[MAX], res[MAX];

Read input dats.

scanf("%d",&n);

for(i = 1; i <= n; i++)

scanf("%d",&in[i]); // [1,2,3,4]

Construct array of prefixes.

pref[0] = 1;

for(i = 1; i <= n; i++) // [1,2,6,24]

pref[i] = pref[i-1] * in[i];

Construct array of suffixes.

suf[n+1] = 1;

for(i = n; i >= 1; i--) // [24,24,12,4]

suf[i] = suf[i+1] * in[i];

Create the resulting array.

for(i = 1; i <= n; i++) // [24,12,8,6]

res[i] = pref[i-1] * suf[i+1];

Print the answer.

for(i = 1; i <= n; i++)

printf("%d ",res[i]);

printf("\n");