973. Maximum sum on a tree

 

Given a tree with n vertices, where the vertex numbered i (1 ≤ i ≤ n) contains ci coins. Select a subset of vertices such that no two of them are adjacent (i.e., connected by an edge), and the sum of coins in the selected vertices is maximized.

 

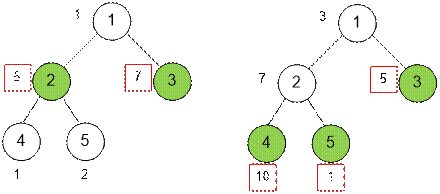
Input. The first line contains the number of vertices n (1 ≤ n ≤ 105) in a tree. Each of the next n – 1 lines contains  two integers u and v (1 ≤ u, v ≤ n), defining an edge in the tree. The last line contains n non-negative integers c1, ... cn – the number of coins in each vertex of the tree.

 

Output. Print the maximum possible sum of coins that can be obtained by selecting a subset of vertices in the tree with no adjacent vertices.

  

Sample input 1

Sample output 1

5

1 2

1 3

2 4

2 5

1 5 7 1 2

12

 

 

Sample input 2

Sample output 2

5

1 2

1 3

2 4

2 5

3 7 5 10 1

16

 

 

SOLUTION

dynamic programmng - trees

 

Algorithm analysis

Let v be a vertex of the tree. Let’s define:

·        dp1(v) as the maximum sum of coins that can be collected from the subtree rooted at v if we take the coins in vertex v.

·        dp2(v) as the maximum sum of coins that can be collected from the subtree rooted at v if we do not take the coins in vertex v.

Then the answer to the problem will be max(dp1(1), dp2(1)), assuming the first vertex is taken as the root of the tree.

 

Let’s define the given functions recursively:

·        If we take the coins in vertex v, then we cannot take coins from its children:

dp1(v) = cv + 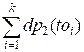, where to1, …, tok are the sons of vertex v.

·        If we do not take the coins in vertex v, then we can choose either to take or not take coins from its children. We select the option with the maximum sum of coins:

dp2(v) = 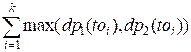, where to1, …, tok are the sons of vertex v.

If v is a leaf with cv coins, then the functions take the following values: dp1(v) = cv and dp2(v) = 0.

 

Example

Let’s assign the labels dp1(v) / dp2(v) to the vertices of the trees from the examples.

 

 

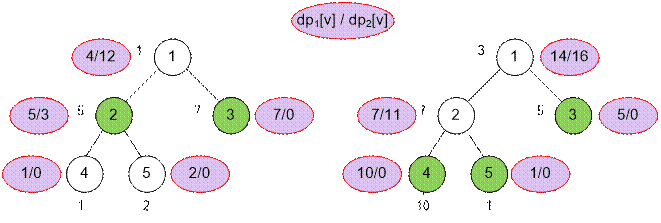
For the first example, we have:

·        dp1(1) = c1 + dp2(2) + dp2(3) = 1 + 3 + 0 = 4;

·        dp2(1) = max(dp1(2), dp2(2)) + max(dp1(3), dp2(3)) = 5 + 7 = 12;

·        dp1(2) = c2 + dp2(4) + dp2(5) = 5 + 0 + 0 = 5;

·        dp2(2) = max(dp1(4), dp2(4)) + max(dp1(5), dp2(5)) = 1 + 2 = 3;

 

For the second example, we have:

·        dp1(1) = c1 + dp2(2) + dp2(3) = 3 + 11 + 0 = 14;

·        dp2(1) = max(dp1(2), dp2(2)) + max(dp1(3), dp2(3)) = 11 + 5 = 16;

·        dp1(2) = c2 + dp2(4) + dp2(5) = 7 + 0 + 0 = 7;

·        dp2(2) = max(dp1(4), dp2(4)) + max(dp1(5), dp2(5)) = 10 + 1 = 11;

 

Exercise

Assign the labels dp1(v) / dp2(v) to the vertices of the tree:

 

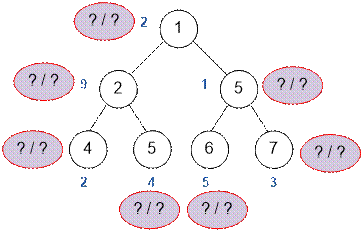
Algorithm realization

Declare the arrays.

 

vector<vector<int> > g;

vector<int> dp1, dp2, cost;

 

The dfs function implements depth-first search. Compute the values of dp1 and dp2 at all vertices of the tree.

 

void dfs(int v, int p = -1)

{

  dp1[v] = cost[v];

  dp2[v] = 0;

 

  for (int to : g[v])

  {

    if (to == p) continue;

 

    dfs(to, v);

 

    dp1[v] += dp2[to];

    dp2[v] += max(dp1[to], dp2[to]);

  }

}

 

The main part of the program. Read the tree and the array of coins.

 

scanf("%d",&n);

g.resize(n+1);

for(i = 1; i < n; i++)

{

  scanf("%d %d",&u,&v);

  g[u].push_back(v);

  g[v].push_back(u);

}

 

dp1.resize(n+1); dp2.resize(n+1);

cost.resize(n+1);

for(i = 1; i <= n; i++)

  scanf("%d",&cost[i]);

 

Let the root of the tree be at vertex 1. Start the depth-first search from there.

 

dfs(1);

 

Compute and print the answer.

 

ans = max(dp1[1], dp2[1]);

printf("%d\n",ans);