975. Floyd
Given a directed
weighted graph. Find a pair of vertices, the shortest distance from one of them
to another is maximum among all pairs of vertices.
Input. The first line contains the
number of vertices n (1 ≤ n ≤ 100). The next n lines of n numbers describe the weighted matrix. Here -1 means no edges
between vertices, and any non-negative number - the presence of an edge of
given weight. All elements on the main diagonal are always zero.
Output. Print the desired
maximum shortest distance.
|
Sample
input |
Sample
output |
|
4 0 5 9 -1 -1 0 2 8 -1 -1 0 7 4 -1 -1 0 |
16 |
SOLUTION
graphs – Floyd - Warsall
Algorithm analysis
In this problem you must implement the
Floyd – Warshall algorithm.
Instead of -1, we put a large positive integer in the cells of the input matrix. Then,
in the matrix of shortest distances, find the largest number – it will be the maximum shortest distance.
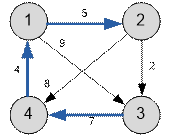
Example
Below given a graph from the
statement. The maximum shortest distance is 16 and is achieved between
vertices 3 and
2.
Algorithm realization
Store the
adjacency matrix of the graph in array g. Plus infinity is assumed to be INF.
#define MAX 101
#define INF 10000000
int g[MAX][MAX];
Function floyd implements the Floyd – Warshall algorithm.
void floyd(void)
{
int i, j, k;
for(k = 0; k
< n; k++)
for(i = 0; i
< n; i++)
for(j = 0; j
< n; j++)
if (g[i][k]
+ g[k][j] < g[i][j]) g[i][j] = g[i][k] + g[k][j];
}
The main part of the program. Read the input graph, build the adjacency matrix g.
scanf("%d",&n);
for(i = 0; i < n; i++)
for(j = 0; j < n; j++)
{
scanf("%d",&g[i][j]);
if (g[i][j]
< 0) g[i][j] = INF;
}
Run the Floyd – Warshall algorithm.
floyd();
In the variable res find the maximum shortest distance
between the pairs of vertices.
for(i = 0; i < n; i++)
for(j = 0; j
< n; j++)
if
((g[i][j] > res) && (g[i][j] < INF)) res = g[i][j];
Print
the answer.
printf("%d\n",res);