976. Флойд - существование
Дан
ориентированный взвешенный граф. По его матрице необходимо для каждой пары
вершин определить, существует кратчайший путь между ними или нет.
Кратчайший путь
может не существовать по двум причинам:
·
Нет ни одного пути.
·
Есть путь сколь угодно маленького веса.
Вход. В первой строке задается количество вершин графа n (1 ≤ n ≤ 100). В следующих n
строках записано по n чисел, задающих
взвешенную матрицу графа (j-ое число
в i-ой строке соответствует весу
ребра из вершины i в вершину j). В ней число 0 обозначает отсутствие
ребра, а любое другое число – наличие ребра соответствующего веса. Все числа по
модулю не превышают 100.
Выход. Выведите n
строк по n чисел: j-ое число в i-ой строке должно быть равно 0, если путь из i в j не существует, 1 –
если существует кратчайший путь, и 2 – если существует путь сколь угодно
маленького веса.
|
Пример
входа |
Пример
выхода |
|
5 0 1 2 0 0 1 0 3 0 0 2 3 0 0 0 0 0 0 0 -1 0 0 0 -1 0 |
1 1 1 0 0 1 1 1 0 0 1 1 1 0 0 0 0 0 2 2 0 0 0 2 2 |
РЕШЕНИЕ
графы –
алгоритм Флойда - Уоршела
Анализ алгоритма
Запустим
алгоритм Флойда – Уоршела на входном графе. Пути между вершинами i и j не существует, если по завершению
алгоритма m[i][j] = +∞. Кратчайшего пути между i и j не существует, если
найдется такая вершина k, что имеются
пути любой величины от i до k и от k до j, а между k и k
имеется цикл отрицательной величины (m[k][k] < 0).
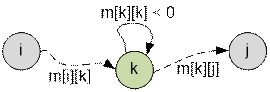
Во всех остальных случаях считаем, что кратчайший путь между i и j существует.
Пример
Граф,
приведенный в примере, имеет вид:
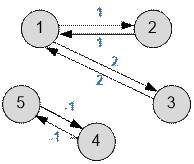
Реализация алгоритма
Матрицу
смежности графа храним в массиве m. В массиве res будем строить результирующую
матрицу. Значение плюс бесконечность положим равным INF.
#define INF 0x3F3F3F3F
#define MAX 101
int m[MAX][MAX], res[MAX][MAX];
Алгоритм Флойда – Уоршела. Поскольку ребра графа имеют
отрицательные веса, то аккуратно их обрабатываем: если на каком-то этапе
обработки m[i][j] станет меньше -INF, то положим m[i][j]
= -INF.
void floyd(void)
{
for(int k = 0; k < n; k++)
for(int i = 0; i < n; i++)
for(int j = 0; j < n; j++)
if
((m[i][k] < INF) && (m[k][j] < INF))
{
if
(m[i][k] + m[k][j] < m[i][j]) m[i][j] = m[i][k] + m[k][j];
if
(m[i][j] < -INF) m[i][j] = -INF;
}
}
Основная часть программы. Читаем
входную матрицу. На диагонали устанавливаем нули. Если между вершинами i и j
нет ребра, то устанавливаем m[i][j] = INF.
scanf("%d",&n);
for(i = 0; i < n; i++)
for(j = 0; j < n; j++)
{
scanf("%d",&m[i][j]);
if ((m[i][j]
== 0) && (i != j)) m[i][j] = INF;
}
Запускаем алгоритм Флойда – Уоршела.
floyd();
Строим результирующую матрицу res. Если
пути между вершинами i и j не существует, то устанавливаем res[i][j]
= 0. Иначе устанавливаем res[i][j] = 1, после чего ищем циклические
пути.
for(i = 0; i < n; i++)
for(j = 0; j < n; j++)
{
if (m[i][j]
== INF) res[i][j] = 0; else
{
res[i][j] = 1;
Между вершинами i и j не существует
кратчайшего пути, если для некоторой вершины k существует путь из i в k и из k в j, а также существует
цикл отрицательной длины, начинающийся и заканчивающийся в вершине k (в ней m[k][k] < 0).
for(k = 0;
k < n; k++)
if
((m[k][k] < 0) && (m[i][k] < INF) && (m[k][j] < INF))
res[i][k] = res[i][j] = res[k][j] = 2;
}
}
Выводим результирующую матрицу res.
for(i = 0; i < n; i++)
{
for(j = 0; j < n; j++)
printf("%d ",res[i][j]);
printf("\n");
}
Java реализация
import java.util.Scanner;
public class Main
{
static final int INF =
100000000;
static int m[][],
res[][];
static int n;
static void floyd()
{
for(int k = 0;
k < n; k++)
for(int i = 0;
i < n; i++)
for(int j = 0;
j < n; j++)
if ((m[i][k]
< INF) && (m[k][j]
< INF))
{
if (m[i][k] + m[k][j]
< m[i][j]) m[i][j] = m[i][k] + m[k][j];
if (m[i][j]
< -INF) m[i][j] = -INF;
}
}
public static void
main(String[] args)
{
Scanner con = new
Scanner(System.in);
n = con.nextInt();
m = new int[n][n];
res = new int[n][n];
for(int i = 0;
i < n; i++)
for(int j = 0;
j < n; j++)
{
m[i][j] = con.nextInt();
if ((m[i][j] ==
0) && (i != j)) m[i][j] = INF;
}
floyd();
for(int i = 0;
i < n; i++)
for(int j = 0;
j < n; j++)
{
if (m[i][j] == INF) res[i][j] =
0; else
{
res[i][j] =
1;
for(int k = 0;
k < n; k++)
if ((m[k][k]
< 0) && (m[i][k]
< INF) && (m[k][j]
< INF)) res[i][k] = res[i][j] = res[k][j] =
2;
}
}
for(int i = 0;
i < n; i++)
{
for(int j = 0;
j < n; j++)
System.out.print(res[i][j] + "
");
System.out.println();
}
con.close();
}
}