976. Floyd
– existence
The directed weighted
graph is given. Using its weighted matrix, determine for each pair of vertices whether
there exists a shortest path between them or not.
The shortest path may not
exist for two reasons:
·
There is no way.
·
There is a way of arbitrarily small weight.
Input. The first line contains the number of vertices n (1 ≤ n ≤ 100). The next n
lines contains n numbers that
describe the weighted matrix (j-th of
the i-th row corresponds to the
weight of the edge from vertex i to
vertex j). The number 0 in this
matrix represents no edge, and any other number – the existence of an edge of
corresponding weight. All the numbers do not exceed 100 by absolute value.
Output. Print n
rows with n numbers: the j-th number in the i-th row must be 0 if the path from i to j does not exist, 1
if there is a shortest path, and 2 if there is a path of arbitrarily small
weight.
|
Sample
input |
Sample
output |
|
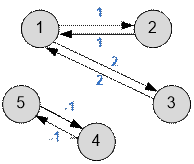
5 0 1 2 0 0 1 0 3 0 0 2 3 0 0 0 0 0 0 0 -1 0 0 0 -1 0 |
1 1 1 0 0 1 1 1 0 0 1 1 1 0 0 0 0 0 2 2 0 0 0 2 2 |
SOLUTION
graphs – Floyd-Warshall
algorithm
Algorithm analysis
Apply the Floyd-Warshall algorithm to the input
graph. A path between the vertices i and j does not exist, if
at the completion of algorithm m[i][j] = +∞. The shortest path between
nodes i and j does not exist, if there is a node k such that there exist the paths of any length from i to k
and from k to j, and between k and k the cycle of negative length exists
(m[k][k] < 0).
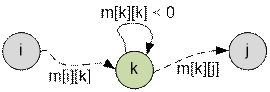
In
all other cases the path between i and
j exists.
Example
Graph given in a sample,
has a form:
Algorithm realization
Store the adjacency matrix
in array m. We shall build the resulting matrix in array res. Let the value
“plus infinity” equals to INF.
#define INF 0x3F3F3F3F
#define MAX 101
int m[MAX][MAX], res[MAX][MAX];
The Floyd-Warshall algorithm.
As the graph vertices have negative weights, process them carefully: if at some
stage of processing m[i][j] becomes less than -INF, set m[i][j]
= -INF.
void floyd(void)
{
for(int k = 0; k < n; k++)
for(int i = 0; i < n; i++)
for(int j = 0; j < n; j++)
if
((m[i][k] < INF) && (m[k][j] < INF))
{
if
(m[i][k] + m[k][j] < m[i][j]) m[i][j] = m[i][k] + m[k][j];
if
(m[i][j] < -INF) m[i][j] = -INF;
}
}
The main part of the program. Read the input adjacency
matrix. Set zeroes on its diagonal. If there is no edge between vertices i and j, set m[i][j] = INF.
scanf("%d",&n);
for(i = 0; i < n; i++)
for(j = 0; j < n; j++)
{
scanf("%d",&m[i][j]);
if ((m[i][j]
== 0) && (i != j)) m[i][j] = INF;
}
Run the Floyd-Warshall algorithm.
floyd();
Build the resulting matrix res. If there is no path
between vertices i and j, set res[i][j] = 0. Otherwise set res[i][j]
= 1, after which look for the cycle paths.
for(i = 0; i < n; i++)
for(j = 0; j < n; j++)
{
if (m[i][j]
== INF) res[i][j] = 0; else
{
res[i][j] = 1;
The shortest path does not exist between the vertices i and j if for some vertex k there
exist a path from i to k and from k to j, and also exists a
cycle of negative length that starts and finishes at vertex k (then m[k][k] < 0).
for(k = 0;
k < n; k++)
if
((m[k][k] < 0) && (m[i][k] < INF) && (m[k][j] < INF))
res[i][k] = res[i][j] = res[k][j] = 2;
}
}
Print the resulting matrix res.
for(i = 0; i < n; i++)
{
for(j = 0; j
< n; j++)
printf("%d ",res[i][j]);
printf("\n");
}
Java realization
import java.util.Scanner;
public class Main
{
static final int INF =
100000000;
static int m[][],
res[][];
static int n;
static void floyd()
{
for(int k = 0;
k < n; k++)
for(int i = 0;
i < n; i++)
for(int j = 0;
j < n; j++)
if ((m[i][k]
< INF) && (m[k][j]
< INF))
{
if (m[i][k] + m[k][j]
< m[i][j]) m[i][j] = m[i][k] + m[k][j];
if (m[i][j]
< -INF) m[i][j] = -INF;
}
}
public static void
main(String[] args)
{
Scanner con = new
Scanner(System.in);
n = con.nextInt();
m = new int[n][n];
res = new int[n][n];
for(int i = 0;
i < n; i++)
for(int j = 0;
j < n; j++)
{
m[i][j] = con.nextInt();
if ((m[i][j] ==
0) && (i != j)) m[i][j] = INF;
}
floyd();
for(int i = 0;
i < n; i++)
for(int j = 0;
j < n; j++)
{
if (m[i][j] == INF) res[i][j] =
0; else
{
res[i][j] =
1;
for(int k = 0;
k < n; k++)
if ((m[k][k]
< 0) && (m[i][k]
< INF) && (m[k][j]
< INF)) res[i][k] = res[i][j] = res[k][j] =
2;
}
}
for(int i = 0;
i < n; i++)
{
for(int j = 0;
j < n; j++)
System.out.print(res[i][j] + "
");
System.out.println();
}
con.close();
}
}