978. Получи дерево
Дан связный
неориентированный граф без петель и кратных ребер. Разрешается удалять из него
ребра. Требуется получить дерево.
Вход. Первая строка содержит два целых числа – количество
вершин n (1 ≤ n ≤ 100) и количество ребер m в графе. Далее следуют m пар целых
чисел, каждая из которых задаёт одно ребро. Гарантируется, что граф связный.
Выход. Выведите n – 1 пару чисел – ребра, входящие в дерево. Ребра
можно выводить в любом порядке.
|
Пример
входа |
Пример
выхода |
|
4 4 1 2 2 3 3 4 4 1 |
1 2 2 3 3 4 |
РЕШЕНИЕ
графы –
поиск в глубину
Анализ алгоритма
Выполним поиск в
глубину, начиная с первой вершины. Строим дерево поиска в глубину и выводим все
его ребра.
Пример
Граф,
приведенный в примере, имеет вид:
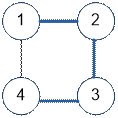
При запуске поиска в
глубину из вершины 1 обход пройдёт по рёбрам: (1, 2), (2, 3),
(3, 4).
Реализация алгоритма
Матрицу смежности графа храним в массиве g.
#define MAX 101
int g[MAX][MAX], used[MAX];
Функция dfs выполняет
поиск в глубину, начиная с вершины v. Выводим каждое ребро (v, i),
входящее в дерево поиска в
глубину.
void dfs(int
v)
{
used[v] = 1;
for (int i = 1; i <= n; i++)
if (g[v][i]
&& !used[i])
{
printf("%d
%d\n",v,i);
dfs(i);
}
}
Основная часть программы. Читаем
входные данные.
scanf("%d %d",&n,&m);
memset(g,0,sizeof(g)); memset(used,0,sizeof(used));
while(m--)
{
scanf("%d
%d",&a,&b);
g[a][b] = g[b][a] = 1;
}
Запускаем поиск в глубину из первой
вершины.
dfs(1);
Java реализация
import java.util.*;
public class Main
{
static int g[][],
used[];
static int n, m;
static void dfs(int v)
{
used[v] =
1;
for(int i = 1;
i <= n; i++)
if (g[v][i] ==
1 && used[i] ==
0)
{
System.out.println(v + "
" + i);
dfs(i);
}
used[v] =
2;
}
public static void
main(String[] args)
{
Scanner con = new
Scanner(System.in);
n = con.nextInt();
m = con.nextInt();
g = new int[n+1][n+1];
used = new int[n+1];
for(int i = 0;
i < m; i++)
{
int a = con.nextInt();
int b = con.nextInt();
g[a][b] = g[b][a] =
1;
}
dfs(1);
con.close();
}
}