978. Get a tree

A connected undirected graph without loops or multiple edges is given. It is allowed to delete edges from the graph. The goal is to obtain a tree.

Input. The first line contains two integers – the number of vertices n (1 ≤ n ≤ 100) and the number of edges m in the graph. The following m pairs of integers each represent an edge. It is guaranteed that the graph is connected.

Output. Print n – 1 pairs of integers – the edges that form a tree. The edges can be printed in any order.

Sample input	Sample output
4 4 1 2 2 3 3 4 4 1	1 2 2 3 3 4

SOLUTION

graphs – depth first search

Algorithm analysis

Perform a depth-first search starting from the first vertex. Build the depth-first search tree and print all of its edges.

Example

The graph given in the example has the following structure:

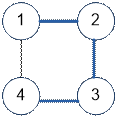
When the depth-first search is started from vertex 1, the traversal will go through the edges: (1, 2), (2, 3), (3, 4).

Algorithm implementation

The adjacency matrix of the graph is stored in the array g.

#define MAX 101

int g[MAX][MAX], used[MAX];

The dfs function performs a depth-first search starting from vertex v.
Each edge (v, i) that is part of the depth-first search tree is printed.

void dfs(int v)

{

int i;

used[v] = 1;

for(i = 1; i <= n; i++)

if (g[v][i] && !used[i])

{

printf("%d %d\n",v,i);

dfs(i);

}

}

The main part of the program. Read the input data.

scanf("%d %d",&n,&m);

memset(g,0,sizeof(g)); memset(used,0,sizeof(used));

while(m--)

{

scanf("%d %d",&a,&b);

g[a][b] = g[b][a] = 1;

}

Start a depth-first search from the first vertex.

dfs(1);

Java implementation

import java.util.*;

public class Main

{

static int g[][], used[];

static int n, m;

static void dfs(int v)

{

used[v] = 1;

for(int i = 1; i <= n; i++)

if (g[v][i] == 1 && used[i] == 0)

{

System.out.println(v + " " + i);

dfs(i);

}

used[v] = 2;

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

n = con.nextInt();

m = con.nextInt();

g = new int[n+1][n+1];

used = new int[n+1];

for(int i = 0; i < m; i++)

{

int a = con.nextInt();

int b = con.nextInt();

g[a][b] = g[b][a] = 1;

}

dfs(1);

con.close();

}

}