981. Минимальный каркас

Определить вес минимального остовного дерева для неориентированного взвешенного связного графа.

Вход. В первой строке находится количество вершин n и рёбер m (1 ≤ n ≤ 100, 1 ≤ m ≤ 6000) в графе. Каждая из следующих m строк содержит тройку чисел a, b, c, где a и b – номера вершин, соединённых ребром, а c – вес ребра (натуральное число, не превышающее 30000).

Выход. Вывести вес минимального остовного дерева.

Пример входа	Пример выхода
3 3 1 2 1 2 3 2 3 1 3	3

РЕШЕНИЕ

графы – минимальное остовное дерево – алгоритм Крускала

Анализ алгоритма

В задаче следует найти вес минимального остовного дерева алгоритмом Крускала.

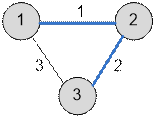
Пример

Граф, приведенный в примере, имеет вид:

Упражнение 1

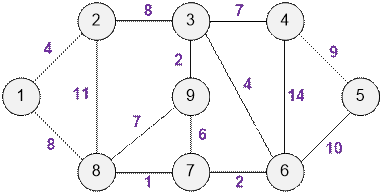
Найдите минимальный остов и его вес для следующего графа.

Упражнение 2

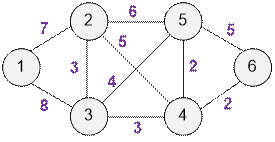
Найдите минимальный остов и его вес для следующего графа.

Реализация алгоритма

Объявим структуру ребра графа (пара вершин и вес ребра). Объявим вектор ребер e.

struct Edge

{

int u, v, dist;

};

vector<Edge> e;

Объявим массив parent, используемый системой непересекающихся множеств.

vector<int> parent;

Функция Repr находит представителя множества, в котором находится вершина n.

int Repr(int n)

{

while (n != parent[n]) n = parent[n];

return n;

}

Функция Union объединяет множества, содержащие элементы x и y.

int Union(int x, int y)

{

x = Repr(x); y = Repr(y);

if (x == y) return 0;

parent[y] = x;

return 1;

}

Функция lt является компаратором для сортировки ребер.

int lt(Edge a, Edge b)

{

return (a.dist < b.dist);

}

Основная часть программы. Инициализация массива parent.

scanf("%d %d",&n,&m);

parent.resize(n + 1);

for (i = 1; i <= n; i++) parent[i] = i;

Читаем ребра графа.

e.resize(m);

for (i = 0; i < m; i++)

scanf("%d %d %d", &e[i].u, &e[i].v, &e[i].dist);

Сортируем ребра по возрастанию весов.

sort(e.begin(), e.end(), lt);

Запускаем алгоритм Крускала построения минимального остова.

res = 0;

for(i = 0; i < m; i++)

if (Union(e[i].u,e[i].v)) res += e[i].dist;

Выводим вес минимального остова.

printf("%d\n",res);

Реализация алгоритма – эвристика

#include <cstdio>

#include <algorithm>

#include <vector>

using namespace std;

struct Edge

{

int u, v, dist;

};

vector<Edge> e;

vector<int> parent, depth;

int i, n, m, res;

int Repr(int n)

{

if (n == parent[n]) return n;

return parent[n] = Repr(parent[n]);

}

int Union(int x, int y)

{

x = Repr(x); y = Repr(y);

if (x == y) return 0;

if (depth[x] < depth[y]) swap(x, y);

parent[y] = x;

if (depth[x] == depth[y]) depth[x]++;

return 1;

}

int lt(Edge a, Edge b)

{

return a.dist < b.dist;

}

int main(void)

{

scanf("%d %d", &n, &m);

parent.resize(n + 1);

depth.resize(n + 1);

for (i = 1; i <= n; i++)

{

parent[i] = i;

depth[i] = 0;

}

e.resize(m);

for (i = 0; i < m; i++)

scanf("%d %d %d", &e[i].u, &e[i].v, &e[i].dist);

sort(e.begin(), e.end(), lt);

res = 0;

for (i = 0; i < m; i++)

if (Union(e[i].u, e[i].v)) res += e[i].dist;

printf("%d\n", res);

return 0;

}

Реализация алгоритма – Прим

#include <cstdio>

#include <cstring>

#include <cmath>

#include <vector>

#include <algorithm>

#define MAX 101

#define INF 0x3F3F3F3F

using namespace std;

int i, n, m, a, b, c, res;

vector<vector<pair<int, int> > > g; // (to, dist)

int used[MAX], dist[MAX];

int Prim(int start)

{

memset(dist, 0x3F, sizeof(dist));

memset(used, 0, sizeof(used));

int i, j, cur = start, res = 0;

dist[cur] = 0;

used[cur] = 1;

for (i = 1; i < n; i++)

{

// cur -> to

for (j = 0; j < g[cur].size(); j++)

{

int to = g[cur][j].first;

int d = g[cur][j].second;

if (!used[to] && (d < dist[to]))

dist[to] = d;

}

int min = INF;

for (j = 1; j <= n; j++)

if (!used[j] && (dist[j] < min))

{

min = dist[j];

cur = j;

}

used[cur] = 1;

res += dist[cur];

}

return res;

}

int main(void)

{

scanf("%d %d", &n, &m);

g.resize(n + 1);

for (i = 0; i < m; i++)

{

scanf("%d %d %d", &a, &b, &c);

g[a].push_back(make_pair(b,c));

g[b].push_back(make_pair(a, c));

}

res = Prim(1);

printf("%d\n", res);

return 0;

}

Java реализация

import java.util.*;

class Edge

{

int u, v, dist;

Edge (int u, int v, int dist)

{

this.u = u;

this.v = v;

this.dist = dist;

}

};

public class Main

{

static int mas[];

static int size[];

static int Repr(int n)

{

if (n == mas[n]) return n;

return mas[n] = Repr(mas[n]);

}

static int Union(int x, int y)

{

x = Repr(x); y = Repr(y);

if(x == y) return 0;

if (size[x] < size[y])

{

int temp = x; x = y; y = temp;

}

mas[y] = x;

size[x] += size[y];

return 1;

}

public static class MyFun implements Comparator<Edge>

{

public int compare(Edge a, Edge b)

{

return a.dist - b.dist;

}

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

int m = con.nextInt();

mas = new int[n+1];

size = new int[n+1];

for(int i = 1; i <= n; i++)

{

mas[i] = i;

size[i] = 1;

}

Vector<Edge> v = new Vector<Edge>();

for(int i = 0; i < m; i++)

{

int x = con.nextInt();

int y = con.nextInt();

int dist = con.nextInt();

v.add(new Edge(x, y, dist));

}

Collections.sort(v, new MyFun());

int res = 0;

for(int i = 0; i < m; i++)

if (Union(v.get(i).u, v.get(i).v) == 1) res += v.get(i).dist;

System.out.println(res);

con.close();

}

}