987. Nails

Some nails are hammered on a straight plank. Any two nails can be joined by a thread. Connect some pairs of nails with a thread, so that to each nail will be tied with at least one thread, and the total length of all threads will be minimal.

Input. The first line contains the number of nails n (1 ≤ n ≤ 100). The next line contains n numbers – the coordinates of all the nails (non-negative integers not exceeding 10000).

Output. Print the minimum total length of all threads.

Sample input	Sample output
5 4 10 0 12 2	6

SOLUTION

dynamic programming

Algorithm analysis

Sort the nail’s coordinates in array а. Let dp[i] equals to the minimal total length of all thread, when any two nails starting from the first one (the nails are numbered starting from 1) till i-th are connected with the thread.

If n = 2, both nails must be joined with the thread, so

dp[2] = a₂ – a₁

If n = 3, we must connect first nail with the second, and second with the third. So

dp[3] = a₃ – a₁

To add i-th nail one has two possibilities to join it with the thread:

1) connect first i – 2 nails among themselves, the (i – 1)-th nail connect to the i-th. The total length of the thread for such connection equals to dp[i – 2] + a[i] – a[i – 1].

2) connect first i – 1 nails among themselves, the i-th nail we connect to the (i – 1)-th. The length of the thread equals to dp[i – 1] + a[i] – a[i – 1].

Select the connection method where the total length of the thread is smallest. So

dp[i] = min(dp[i – 2], dp[i – 1]) + a[i] – a[i – 1]

Sample

Sort the nail’s coordinates for the sample input: 0, 2, 4, 10, 12. For two nails dp[2] = 2 – 0 = 2. For three nails we must connect them all with the thread (each nail must be tied with at least one thread), so

dp[3] = (4 – 2) + (2 – 0) = 4

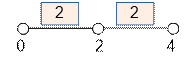
Let’s calculate the optimal length of the thread for 4 nails:

dp[4] = min(dp[2], dp[3]) + 10 – 4 = 2 + 6 = 8

For 5 nails the minimum possible length of the thread equals to

dp[5] = min(dp[3], dp[4]) + 12 – 10 = 4 + 2 = 6

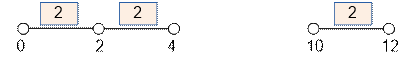
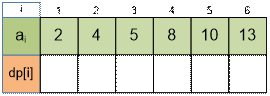
Exercise

Find the values of dp[i] for the next input data:

Algorithm realization

Array а contains the nail’s coordinates. Declare the resulting array dp.

#define MAX 101

int a[MAX], dp[MAX];

Read the input data.

scanf("%d",&n);

for(i = 1; i <= n; i++)

scanf("%d",&a[i]);

Sort the nail’s coordinates.

sort(a+1,a+n+1);

Initialize dp[2] and dp[3].

dp[2] = a[2] - a[1];

dp[3] = a[3] - a[1];

Calculate the values of cells in dp array using formula.

for(i = 4; i <= n; i++)

dp[i] = min(dp[i-1],dp[i-2]) + a[i] - a[i-1];

Print the answer.

printf("%d\n",dp[n]);

Java realization

import java.util.*;

class Main

{

static int a[] = new int[101];

static int dp[] = new int[101];

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

for (int i = 1; i <= n; i++)

a[i] = con.nextInt();

Arrays.sort(a,1,n+1);

dp[2] = a[2] - a[1];

dp[3] = a[3] - a[1];

for(int i = 4; i <= n; i++)

dp[i] = Math.min(dp[i-1],dp[i-2]) + a[i] - a[i-1];

System.out.println(dp[n]);

con.close();

}

}