992. Города и дороги

В галактике “Milky Way” на планете “Neptune” есть n городов, некоторые из которых соединены дорогами. Император “Maximus” галактики “Milky Way” решил провести инвентаризацию дорог на планете “Neptune”. Но, как оказалось, он не силен в математике, поэтому просит Вас сосчитать количество дорог.

Вход. В первой строке записано число n (0 ≤ n ≤ 100). В следующих n строках записано по n чисел, каждое из которых является единицей или нулем. Если в позиции (i, j) квадратной матрицы стоит единица, то i-ый и j-ый города соединены дорогой, а если ноль, то не соединены.

Выход. Выведите одно число – количество дорог на планете “Neptune”.

Пример входа	Пример выхода
5 0 1 0 0 0 1 0 1 1 0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0	3

РЕШЕНИЕ

графы

Анализ алгоритма

Пусть g – матрица смежности графа. Поскольку граф неориентированный, то в случае наличия ребра между вершинами i и j имеем равенства:

g[i][j] = g[j][i] = 1

Количество ребер в графе равно числу единиц в матрице смежности, деленное на 2.

Пример

Граф, приведенный в примере, имеет вид:

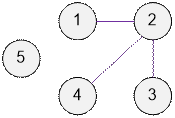
Количество дорог на планете равно 3.

Реализация алгоритма

Читаем входное значение n.

scanf("%d",&n);

Читаем матрицу смежности. Вычисляем сумму чисел res в ней. Поскольку граф неориентированный, то res равно удвоенному количеству ребер.

res = 0;

for(i = 0; i < n; i++)

for(j = 0; j < n; j++)

{

scanf("%d",&val);

res += val;

}

Вычисляем и выводим количество ребер.

res /= 2;

printf("%d\n",res);

Java реализация

import java.util.*;

public class Main

{

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

int res = 0;

for(int i = 0; i < n; i++)

for(int j = 0; j < n; j++)

res += con.nextInt();

res /= 2;

System.out.println(res);

con.close();

}

}

Python реализация – на лету

Читаем входное значение n.

n = int(input())

Сумму чисел в матрице смежности вычисляем в переменной res.

res = 0

Читаем матрицу смежности строка за строкой. Для каждой строки вычисляем сумму чисел в ней. Затем прибавляем эту сумму к значению res.

for _ in range(n):

res += sum(map(int, input().split()))

Поскольку граф неориентированный, то сумма res равна удвоенному количеству ребер. Делим res на 2 и выводим ответ.

res //= 2

print(res)

Python реализация – матрица смежности

Читаем входные данные.

n = int(input())

g = [[int(j) for j in input().split()] for i in range(n)]

Вычисляем сумму чисел s в матрице смежности. Поскольку граф неориентированный, то s равно удвоенному количеству ребер.

s = 0

for row in g:

s += sum(row)

Выводим количество ребер.

print(s // 2)