993. Светофоры

В подземелье имеется m тоннелей и n перекрёстков. Каждый тоннель соединяет два перекрёстка. Крысиный Король решил установить светофор в каждом тоннеле перед каждым перекрёстком.

Напишите программу, которая определит, сколько светофоров необходимо установить на каждом перекрёстке. Перекрёстки пронумерованы от 1 до n.

Вход. Первая строка содержит два целых числа n и m (0 < n ≤ 100, 0 ≤ m ≤ n · (n – 1) / 2). Каждая из следующих m строк содержит два целых числа i и j (1 ≤ i, j ≤ n), означающие, что перекрёстки i и j соединены тоннелем.

Выход. Выведите n чисел: k-е число – это количество светофоров, которые необходимо установить на k-м перекрёстке.

Гарантируется, что между любыми двумя перекрёстками существует не более одного тоннеля, и отсутствуют тоннели, соединяющие перекрёсток с самим собой.

Пример входа	Пример выхода
7 10 5 1 3 2 7 1 5 2 7 4 6 5 6 4 7 5 2 1 5 3	3 3 2 2 5 2 3

РЕШЕНИЕ

графы

Анализ алгоритма

Система перекрёстков и тоннелей естественным образом задаёт граф: перекрёстки являются вершинами, а тоннели – рёбрами. Поскольку тоннели двунаправленные, граф является неориентированным.

Количество светофоров, устанавливаемых на k-м перекрёстке, равно степени вершины k, то есть числу тоннелей, инцидентных этому перекрёстку.

Заведём массив ton, где ton[k] – количество тоннелей, прилегающих к k-му перекрёстку. Тогда для каждого неориентированного ребра (a, b) необходимо увеличить значения ton[a] и ton[b] на единицу.

Пример

Граф, приведённый в примере, имеет следующий вид:

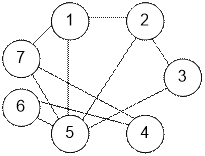
Реализация алгоритма

Объявим массив ton, в котором будем хранить информацию о тоннелях.

#define MAX 110

int ton[MAX];

Читаем входные данные. Последовательно обрабатываем каждый тоннель, увеличивая степени соответствующих вершин графа.

scanf("%d %d",&n,&m);

memset(ton,0,sizeof(ton));

for (i = 0; i < m; i++)

{

scanf("%d %d",&a,&b);

ton[a]++; ton[b]++;

}

Выводим количество светофоров, необходимых на каждом перекрёстке.

for (i = 1; i <= n; i++)

printf("%d ",ton[i]);

printf("\n");