10030. SpaceX
Илон Маск планирует отправить свои космические
корабли на k различных планет. Для
этого у него есть n космических
кораблей. Изначально известно, куда будет отправлен каждый корабль. Планеты
пронумерованы от 1 до 109 . Как главному космоинженеру компании
SpaceX, вам предоставлено право менять пункт назначения любого корабля. Вам, за
минимальное количество изменений, нужно сделать так, чтобы все корабли были
отправлены на k различных планет.
Вход. В первой строке даны два числа n (1 ≤ n ≤ 105) и k (1 ≤ k ≤ n). Во второй строке расположены n целых чисел pi (1 ≤ pi
≤ 105) – изначальные пункты назначения кораблей.
Выход. Выведите минимальное количество изменений.
|
Пример входа 1 |
Пример выхода 1 |
|
3 1 1 5 3 |
2 |
|
|
|
|
Пример входа 2 |
Пример выхода 2 |
|
5 4 10 1 2 1 10 |
1 |
РЕШЕНИЕ
структура данных map
Анализ алгоритма
Для
каждого пункта назначения p в отображении m подсчитаем количество кораблей m[p], отправленных туда. Например, во
втором тесте две ракеты отправлены на планету 1, одна ракета отправлена на
планету 2, и две ракеты отправлены на планету 10. Структура map имеет следующий вид:
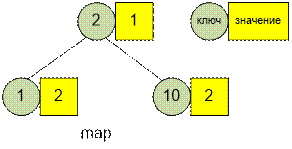
Размер отображения m.size() = 3, все корабли
отправены на 3 планеты. Корабли следует отправить в точности на k = 4 различных
планет. Если m.size() < k, то k – m.size() кораблям
следует сменить курс.
Рассмотрим
случай, когда космические корабли отправлены на более чем k планет. Пусть k = 4, но
структура map будет
следующей:
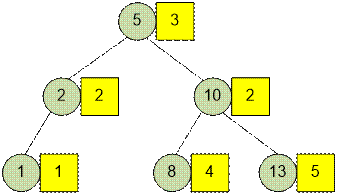
17 кораблей отправлены на 6 планет. Из двух планет следует перенаправить
корабли на любые из 4 оставшихся. Поскольку требуется минимизировать количество изменений, то следует
найти две планеты, на которые отправлены наименьшее количество кораблей.
Отсортируем числа – количество кораблей, отправленные на планеты. И найдем
сумму двух наименьших.

Реализация алгоритма
Объявим
структуры данных.
map<long long, long long> m;
vector<long long> v;
Читаем
входные данные.
scanf("%d %d", &n, &k);
for (i = 0; i < n; i++)
{
scanf("%d", &x);
В m[x] подсчитываем количество кораблей, отправленных на
планету x.
m[x]++;
}
Если
все космические корабли отправлены менее чем на k планет, то минимальное количество изменений равно k – m.size().
if (m.size() < k)
{
printf("%d\n", k - m.size());
return 0;
}
Космические
корабли отправлены более чем на k
планет. Строим вектор v, содержащий
количество кораблей, отправленных на разные планеты.
for (iter = m.begin(); iter != m.end(); iter++)
v.push_back((*iter).second);
Сортируем
вектор v.
sort(v.begin(), v.end());
Ищем
сумму m.size() – k наименьших чисел (именно с такого количества планет следует
изменить курс ракет).
sum = 0;
for (i = 0; i < m.size() - k; i++)
sum += v[i];
Выводим
ответ.
printf("%lld\n", sum);