10056. Breadth First Search 0 – 1
An undirected
graph is given. The weight of its edges can be 0 or 1 only.
Find the shortest distance between vertices s and d.
Input. The first line
contains four integers: the number of vertices n, the number of edges m
(n, m ≤ 105), and the vertex numbers s and
d (1 ≤ s, d ≤ n). Each of the following m lines
contains three integers a, b, and w, representing an
undirected edge (a, b) with an integer weight w (0 ≤
w ≤ 1).
Output. Print the
shortest distance between vertices s and d.
|
Sample
input |
Sample
output |
|
5 5 1 3 1 2 0 2 3 1 3 4 0 4 5 1 1 5 1 |
1 |
SOLUTION
breadth first search
Algorithm analysis
0-1
Breadth-First Search (or 0-1 BFS) is a modification of the classic
Breadth-First Search (BFS) algorithm, used for finding shortest paths in
graphs. The key difference of this algorithm is that the edge weights in the
graph can only be 0 or 1, allowing for a significant optimization in search
efficiency.
Problem
Statement. Imagine we have a weighted graph where the edge weights
are either 0 or 1. For example, such a graph can represent a city where certain
roads are free (weight 0), while others have a toll (weight 1). Our goal is to
find the shortest path from one vertex to another, taking these weights into
account.
Limitations of
the Standard Breadth-First Search Algorithm. The classic BFS
algorithm has a complexity of O(V + E) and is used to find shortest paths in
unweighted graphs, but it only works effectively when all edges have the same
weight. If edge weights vary, this approach becomes inefficient. Typically,
Dijkstra's algorithm is used for weighted graphs, with a complexity of O(V2 + E) or O(E * log2V). However, for
graphs with edge weights of only 0 and 1, there is a faster approach – 0-1 BFS.
0-1 BFS Algorithm
In 0-1 BFS, we use a double-ended
queue (deque). The idea is as follows:
1.
We start from the initial vertex start and add it to
the deque with an initial distance of 0.
2.
When processing each vertex u (which is dequeued from
the front), we examine its neighbors v:
o
If the edge (u, v) has a weight of 0, the neighboring vertex v is added to the front of the
deque with the current distance (dist[v]
= dist[u]).
o
If the edge (u, v) has a weight of 1, the neighboring vertex v is added to the back of the
deque with an increased distance of one (dist[v] = dist[u] + 1).
3.
This ensures an efficient order of vertex processing:
vertices reachable through edges with smaller weights are processed earlier.
Thus, the use of a
double-ended queue guarantees that we always have access to the vertex with the
minimum distance at the front of the deque, and the algorithm’s complexity
remains O(V + E).
Edge relaxation in 0-1 BFS
is similar to the classical relaxation in Dijkstra’s algorithm but differs in
that it uses a deque instead of a priority queue to order vertices based on
edge weights.
Let’s consider the
following example. Initialize the array of shortest distances dist and
the queue q:
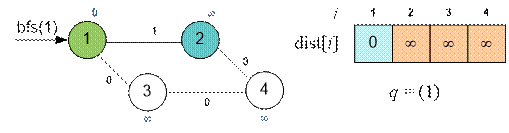
Examine the edges
originating from vertex 1 and relax the edges (1, 2) and (1, 3). Vertex 3 will
be added to the front of the queue, while vertex 2 will be added to the back of
the queue.
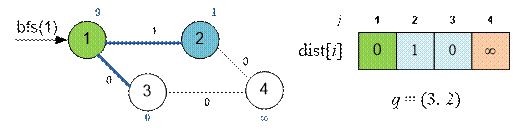
However, the value dist[2]
= 1 is not final. Traverse edge 3 – 4 and set dist[4] = 0, making the queue q =
(4, 2). Then, examine edge 4 – 2, and the value dist[2] is updated to 0. Thus, dist[2]
took on two different values as a result of relaxation (first 1, then 0).
Example
The graph given in the
example looks as follows:
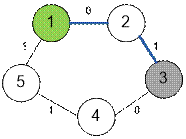
The length of the shortest
path from vertex 1 to vertex 3 is 1, and the shortest path is as follows: 1 – 2
– 3.
Algorithm realization
Declare the constant
infinity.
#define INF
0x3F3F3F3F
Declare the array of
shortest distances dist and the adjacency list
of the graph g.
vector<int>
dist;
vector<vector<pair<int, int>
> > g;
The bfs function implements breadth-first search from the vertex start.
void bfs(int start)
{
Initialize the array of shortest distances dist.
dist = vector<int>(n
+ 1, INF);
dist[start] = 0;
Declare a queue and enqueue the starting vertex start.
deque<int>
q;
q.push_back(start);
Continue the breadth-first search algorithm while the queue is not empty.
while
(!q.empty())
{
Extract the vertex v from the front of the queue.
int v = q.front(); q.pop_front();
Iterate through the edges outgoing from vertex v.
for (auto edge : g[v])
{
int to = edge.first;
int w = edge.second;
The current edge (v, to) has a weight w. Perform its
relaxation.
if
(dist[to] > dist[v] + w)
{
If the edge is relaxed, recalculate the shortest distance dist[to].
dist[to] = dist[v] + w;
Depending on the weight of the edge w, add vertex to to the
end or the front of the queue.
if (w == 1)
q.push_back(to);
else
q.push_front(to);
}
}
}
}
The main part of the program. Read the input data.
scanf("%d %d %d %d",
&n, &m, &s, &d);
g.resize(n + 1);
Read the graph.
for (i = 0; i < m; i++)
{
scanf("%d
%d %d", &a, &b, &w);
g[a].push_back({ b, w });
g[b].push_back({ a, w });
}
Start the breadth-first search from the starting vertex s.
bfs(s);
Print the shortest distance to vertex d.
printf("%d\n",
dist[d]);