10058. Breadth First Search 0 – 1 – 2
Undirected graph is given.
The weights of its edges can be 0, 1, or 2 only. Find the
shortest distance from source s to
destination d.
Input.
First line contains four integers: number of vertices n, number of edges m (n, m ≤ 105), source s and destination d (1 ≤ s, d ≤ n). Each of the next m lines contains three integers a, b and
w describing an undirected edge (a, b) with weight w (0 ≤ w ≤ 2).
Output. Print the shortest distance from s to d.
|
Sample input |
Sample output |
|
5 5 1 4 1 2 1 2 3 0 3 4 2 1 5 2 4 5 2 |
3 |
SOLUTION
graphs – breadth first
search
Algorithm analysis
For each edge (u, v) of weight 2, we introduce a
fictitious vertex p and replace it
with two edges of weight 1: (u, p) and (p, v). Initially, the
vertices of the graph are numbered 1, 2,…., n.
Vertices n + 1, n + 2,… will be declared fictitious. Since there are at most m edges in the graph, there will be at
most m fictitious vertices.

Problem is reduced to breadth-first
search on 0 - 1 graph.
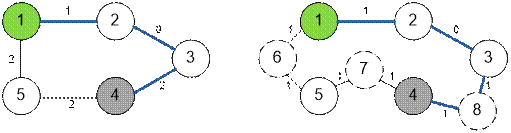
Example
The sample graph is
shown on the left. For each edge with weight 2, we introduce a fictitious
vertex (vertices 6, 7, 8 are fictitious). On the right you can see a 0 – 1 graph.

Algorithm realization
Declare a
constant infinity.
#define INF 0x3F3F3F3F
Declare
an array of shortest distances dist and
an adjacency list of the graph g.
vector<int> dist;
vector<vector<pair<int, int> > > g;
Function
bfs
implements the breadth first search on 0 – 1 graph from the vertex start.
void bfs(int start)
{
dist = vector<int>(n + 1, INF);
dist[start] = 0;
deque<int> q;
q.push_back(start);
while (!q.empty())
{
int v = q.front();
q.pop_front();
for (int i = 0; i < g[v].size(); i++)
{
int to = g[v][i].first;
int w = g[v][i].second;
if (dist[to] > dist[v] + w)
{
dist[to] = dist[v] + w;
if (w == 1)
q.push_back(to);
else
q.push_front(to);
}
}
}
}
The main part of the program. Read the input
data. Build a
graph.
scanf("%d %d %d %d", &n, &m, &s, &d);
The resulting graph, taking into account the fictitious
vertices, will contain at most n + m vertices.
g.resize(n + m + 1);
for (i = 0; i < m; i++)
{
scanf("%d %d
%d", &a, &b, &w);
if (w <= 1)
{
g[a].push_back(make_pair(b,
w));
g[b].push_back(make_pair(a,
w));
}
else
{
Process
an edge of length 2. Create
a fictitious vertex, increase the number of vertices by 1.
n++;
Construct
the undirected edges (a, n), (n,
b) of weight 1.
g[a].push_back(make_pair(n, 1));
g[n].push_back(make_pair(b, 1));
g[b].push_back(make_pair(n, 1));
g[n].push_back(make_pair(a, 1));
}
}
Run
the breadth first search from the starting vertex s.
bfs(s);
Print the
shortest path to the vertex
d.
printf("%d\n", dist[d]);