10112. Tree Balanced

Given a binary tree. Determine if it is height-balanced. A height-balanced binary tree is defined as a binary tree in which the depth of the two subtrees of every node never differs by more than 1.

Definition of a tree:

//Java

class TreeNode {

int val;

TreeNode left;

TreeNode right;

TreeNode(int x) {

val = x;

left = null;

right = null;

}

}

// C++

class TreeNode

{

public:

int val;

TreeNode *left;

TreeNode *right;

TreeNode(int x) : val(x), left(NULL), right(NULL) {}

};

Implement function isBalanced that returns true if tree is balanced and false otherwise.

// Java

int isBalanced(TreeNode tree)

// C++

int isBalanced(TreeNode *tree)

Example

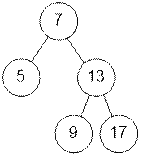
Function isBalanced returns true because tree is balanced.

SOLUTION

binary tree

Algorithm analysis

Let Height be a function that returns the height of the tree (the number of vertices from the root to the farthest leaf). However, if the tree is not balanced, then function Height returns -1.

For each vertex root you should calculate:

· the height of the left subtree Left;

· the height of the right subtree Right;

If either Left or Right is -1, then the tree root is not balanced. The tree root will also be not balanced if | Left – Right | > 1.

The original tree root will be balanced if its height is not -1.

Algorithm realization

bool isBalanced(TreeNode* root)

{

return (Height(root) != -1);

}

If tree root is not balanced, function Height returns -1.

If tree root is balanced, function Height returns the height of the tree (the number of vertices from the root to the farthest leaf).

int Height(TreeNode* root)

{

If root = NULL, the height of the tree is 0.

if (root == NULL) return 0;

Find the height of the left Left and right Right subtree.

int Left = Height(root->left);

int Right = Height(root->right);

The tree is not balanced, if one of the following conditions is true:

· left subtree is not balanced (Left = -1);

· right subtree is not balanced (Right = -1);

· the absolute value of difference of subtrees heights is greater than 1.

if (Left == -1 || Right == -1 || abs(Left - Right) > 1) return -1;

return max(Left, Right) + 1;

}

Java realization

boolean isBalanced(TreeNode tree)

{

return (Height(tree) != -1);

}

int Height(TreeNode tree)

{

if (tree == null) return 0;

int Left = Height(tree.left);

int Right = Height(tree.right);

if (Left == -1 || Right == -1 || Math.abs(Left - Right) > 1)

return -1;

return Math.max(Left, Right) + 1;

}