10117. Треугольники
Фермер Джон хочет сделать
треугольное пастбище.
Имеется n столбов забора как различных точек (x1, y1),
..., (xn, yn) на карте фермы. Он может
выбрать три из них для формирования вершин треугольного пастбища, так чтобы
одна из сторон была параллельна оси x,
а другая параллельна оси y.
Какую максимальную площадь
пастбища может получить Фермер Джон?
Вход.
Первая строка содержит целое число n (3
≤ n ≤ 100). Каждая из
последующих n строк содержит два
целых числа xi и yi, каждое в интервале [-104,
104] включительно, описывающих размещение столба изгороди.
Выход.
Поскольку площадь может получиться не целой, выведите целое число – удвоенную максимальную
площадь, которую может получить Фермер Джон.
|
Пример входа |
Пример выхода |
|
4 0 0 0 1 1 0 1 2 |
2 |
РЕШЕНИЕ
геометрия - перебор
Анализ алгоритма
Поскольку
одна сторона
пастбища должна быть параллельна оси x,
а другая параллельна оси y, то
само пастбище имеет форму прямоугольного треугольника.
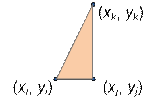
Переберем тройки точек (i, j, k) – вершин
треугольника. Предполагаем, что вершина (xj, yj) является прямым углом, точки
j и k лежат на одной вертикали, а
точки i и j лежат на одной горизонтали. Для этого должно выполняться yi = yj и xi = xk.
Из всех возможных троек (i, j, k) ищем такую, для которой
площадь треугольника будет наибольшей. Удвоенная площадь треугольника (именно
ее следует вывести) равна модулю произведения его катетов, а именно
| (xj – xi) * (yk – yi)
|
Пример
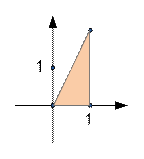
В первом примере фермер Джон
может сделать треугольное пастбище с удвоенной максимальной площадью 2.
Реализация алгоритма
Координаты точек храним в массивах x и y.
#define MAX 100
long long x[MAX], y[MAX];
Читаем входные данные.
scanf("%d", &n);
for (i = 0; i < n; i++)
scanf("%lld
%lld", &x[i], &y[i]);
В переменной best подсчитываем удвоенную максимальную площадь треугольного пастбища.
best = -1;
Искомое пастбище имеет форму прямоугольного треугольника. Перебираем
тройки точек (i, j, k),
предполагая что вершина (xj, yj) является прямым углом, точки
j и k лежат на одной вертикали, а
точки i и j лежат на одной горизонали.
for (i = 0; i < n; i++)
for (j = 0; j < n; j++)
for (k = 0; k < n; k++)
if (y[i] == y[j]
&& x[i] == x[k])
{
Вычисляем площадь треугольника.
area = (x[j] - x[i]) * (y[k] -
y[i]);
if (area < 0)
area *= -1;
Среди всех возможных треугольников ищем треугольник с наибольшей
площадью.
if (area >
best) best = area;
}
Выводим ответ.
printf("%lld\n", best);