10117. Triangles

Farmer John would like to create a triangular pasture for his cows. There are n fence posts at distinct points (x₁, y₁), ..., (x_n, y_n) on the 2D map of his farm. He can choose three of them to form the vertices of the triangular pasture as long as one of the sides of the triangle is parallel to the x-axis and another side is parallel to the y-axis.

What is the maximum area of a pasture that Farmer John can form? It is guaranteed that at least one valid triangular pasture exists.

Input. The first line contains the integer n (3 ≤ n ≤ 100). Each of the next n lines contains two integers x_i and y_i, each in the range [-10⁴, 10⁴] inclusive, describing the location of a fence post.

Output. As the area itself is not necessarily an integer, output two times the maximum area of a valid triangle formed by the fence posts.

Sample input	Sample output
4 0 0 0 1 1 0 1 2	2

SOLUTION

geometry – full search

Algorithm analysis

Since one side of the pasture must be parallel to the x-axis and the other parallel to the y-axis, the pasture itself has the shape of a right-angled triangle.

Iterate over the triples of points (i, j, k), the vertices of triangle. Assume that the vertex (x_j, y_j) is a right angle, points j and k lie on the same vertical, and points i and j lie on the same horizontal. For this, y_i = y_j and x_i = x_k must be satisfied.

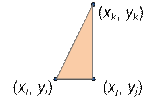
From all possible triplets (i, j, k) we are looking the one for which the area of triangle is the largest. The doubled area of triangle (that must be printed) equals to the absolute value of the product of its legs, namely

| (x_j – x_i) * (y_k – y_i) |

Example

In the first sample farmer John can form a triangular pasture with a twice maximum area of 2.

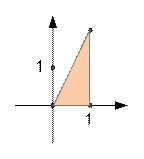
Algorithm realization

The coordinates of the points store in arrays x and y.

#define MAX 100

long long x[MAX], y[MAX];

Read the input data.

scanf("%d", &n);

for (i = 0; i < n; i++)

scanf("%lld %lld", &x[i], &y[i]);

In the variable best compute the twice maximum area of a triangular pasture.

best = -1;

The desired pasture has the shape of a right angled triangle. Iterate through the triples of points (i, j, k), assuming that the vertex (x_j, y_j) is a right angle, points j and k lie on the same vertical, and points i and j lie on the same horizontal.

for (i = 0; i < n; i++)

for (j = 0; j < n; j++)

for (k = 0; k < n; k++)

if (y[i] == y[j] && x[i] == x[k])

{

Compute the area of triangle.

area = (x[j] - x[i]) * (y[k] - y[i]);

if (area < 0) area *= -1;

Among all possible triangles find the triangle with the largest area.

if (area > best) best = area;

}

Print the answer.

printf("%lld\n", best);