10119. Swapity swap
Farmer John’s n
cows are standing in a line. The i-th cow from the left has label i (1
≤ i ≤ n). Farmer John has come up with a new morning
exercise routine for the cows. He tells them to repeat the following two-step
process exactly k times:
·
The sequence of cows currently in positions a1, …, a2 from the left reverse their order. Then, the
sequence of cows currently in positions b1, …, b2
from the left reverse their order.
After the cows have
repeated this process exactly k times, output the label of the i-th
cow from the left for each i (1 ≤ i ≤ n).
Input. The first line of
contains n (1 ≤ n ≤ 100) and
k (1 ≤ k
≤ 109). The second line contains a1 and
a2 (1 ≤ a1 < a2
≤ n), and the third line contains
b1 and b2
(1 ≤ b1 < b2 ≤ n).
Output. On the i-th
line of output, print the label of the i-th cow from the left at the end
of the exercise routine.
|
Sample input |
Sample output |
|
7 2 2 5 3 7 |
1 2 4 3 5 7 6 |
SOLUTION
simulation
Algorithm analysis
If we simulate the
process of rearranging cows, we will obtain Time Limit, since the number of
repetitions of the two-step process k ≤ 109 is too
large.
Let’s place the
cows in order at positions from 1 to n. For each cow number i (1 ≤ i ≤ n), we find the position in which it will end up after k
iterations. For each cow, we find the number of iterations p, after
which it will again occupy its original place. This number p ≤
n ≤ 100 is not large. Then
this cow will take the original place after 2p, 3p, 4p ... iterations.
After k – (k % p) iterations, the considered cow will
again be in its original place (since the specified number is divisible by p).
It remains to perform another k % p iterations to find the final
position of the cow.
Example
The initial order
of the cows is:
![]()
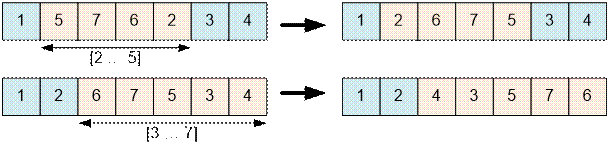
Step 1
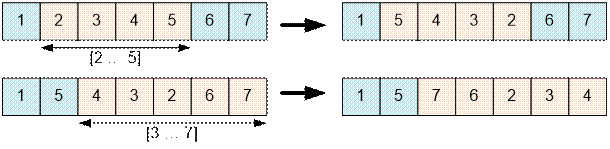
Step 2
Algorithm realization
Declare an array
pos. If cow number i after k iterations takes position cur,
then we assign pos[cur] = i.
int pos[101];
Let some cow be at position x. The function nex(x)
returns the position of this cow after the two-step process. If the cow is at
position x, that belongs to the segment [a1; a2], then after reversing it the
cow will be moved to position a1 + a2 – x.
int nex(int x)
{
if (a1 <= x && x <= a2) x = a1 + a2 - x;
if (b1 <= x && x <= b2) x = b1 + b2 - x;
return x;
}
The main part of the program. Read the input data.
scanf("%d %d", &n, &k);
scanf("%d %d", &a1, &a2);
scanf("%d %d", &b1, &b2);
For each cow number i, we find its position after completing the
process of all exchanges.
for (i = 1; i <= n; i++)
{
In the variable p we find the number of iterations (one iteration
is performing the two-step process once) after which the i-th cow will
be in its place again. The variable cur contains the current position of
the cow.
p = 1; cur = nex(i);
Execute the loop until the i-th cow returns to its starting place
– position number i.
while (cur != i)
{
p++;
cur = nex(cur);
}
After k – (k % p) iterations, the i-th cow
will again be in the i-th place. Execute another k % p
iterations to find the final location of the i-th cow.
kk = k % p;
for (j = 0; j <
kk; j++)
cur = nex(cur);
Cow number i will take position cur after k
iterations.
pos[cur] = i;
}
Print the final location of the cows after all exchanges are completed.
for (i = 1; i <= n; i++)
printf("%d\n", pos[i]);
Algorithm realization – Time Limit
In the case of naive simulation of operations, due to the limit k
≤ 109, we get Time Limit.
#include <cstdio>
#include <algorithm>
using namespace std;
int i, n, k, a1, a2, b1, b2;
int m[101];
int main(void)
{
scanf("%d
%d", &n, &k);
scanf("%d
%d", &a1, &a2);
scanf("%d
%d", &b1, &b2);
for (i = 1; i <=
n; i++)
m[i] = i;
for (i = 0; i <
k; i++)
{
reverse(m + a1, m + a2 +
1);
reverse(m + b1, m + b2 +
1);
}
for (i = 1; i <=
n; i++)
printf("%d\n", m[i]);
return 0;
}