10147. Tree Предыдущий

Дано бинарное дерево.  Найдите Предыдущий элемент для заданного.

Определение дерева:

//Java

class TreeNode {

int val;

TreeNode left, right, parent;

TreeNode(int x, TreeNode prev) {

val = x;

left = null;

right = null;

parent = prev;

}

}

// C++

class TreeNode

{

public:

int val;

TreeNode *left, *right, *parent;

TreeNode(int x, TreeNode *prev = NULL) : val(x), left(NULL), right(NULL), parent(prev) {}

};

Реализуйте функцию Prev которая возвращает указатель на предыдущий элемент в дереве. Если предыдущий элемент не существует, верните NULL.

// Java

TreeNode Prev(TreeNode tree)

// C++

TreeNode* Prev(TreeNode *tree)

Пример

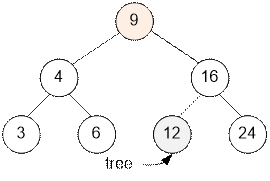
Функция Prev для tree указывающего на 12, возвращает указатель на вершину со значением 9.

РЕШЕНИЕ

дерево

Анализ алгоритма

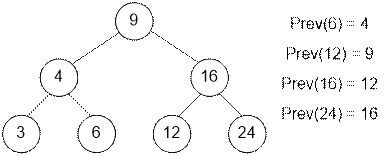
Если существует левое поддерево для tree, то предыдущим элементом является максимальный элемент в нем.

Иначе следует подниматься вверх пока не найдем вершину, которая будет правым сыном своего родителя. Этот родитель и будет предыдущим элементом.

Реализация алгоритма

Объявим функцию максимума. Для нахожденя максимума в дереве двигаемся от корня все время в правого сына пока не найдем такую вершину, правый сын которой равен NULL.

TreeNode *Maximum(TreeNode *tree)

{

if (tree == NULL) return tree;

while (tree->right != NULL) tree = tree->right;

return tree;

}

Функция Prev находит предыдущий элемент.

TreeNode *Prev(TreeNode *tree)

{

Если существует левое поддерево, то предыдущим элементом является максимальный элемент в нем.

if (tree->left != NULL) return Maximum(tree->left);

Иначе следует подниматься вверх пока не найдем вершину, которая будет правым сыном своего родителя. Этот родитель и будет предыдущим элементом.

TreeNode *Prev = tree->parent;

while ((Prev != NULL) && (tree == Prev->left))

{

tree = Prev;

Prev = Prev->parent;

}

return Prev;

}

Java реализация

TreeNode Maximum(TreeNode tree)

{

if (tree == null) return tree;

while (tree.right != null) tree = tree.right;

return tree;

}

TreeNode Prev(TreeNode tree)

{

if(tree.left != null) return Maximum(tree.left);

TreeNode Prev = tree.parent;

while ((Prev != null) && (tree == Prev.left))

{

tree = Prev;

Prev = Prev.parent;

}

return Prev;

}