10151. Cow contest

n cows, numbered from 1 to n, participate in a programming contest. As we all know, some cows code better than others. Each cow has a certain constant skill rating that is unique among the competitors.

The contest is conducted in several head-to-head rounds, each between two cows. If cow a has a greater skill level than cow b (1 ≤ a, b ≤ n, a ≠ b), then cow a will always beat cow b.

Farmer John is trying to rank the cows by skill level. Given a list the results of m two-cow rounds, determine the number of cows whose ranks can be precisely determined from the results. It is guaranteed that the results of the rounds will not be contradictory.

Input. The first line contains two integers n (1 ≤ n ≤ 100) and m (1 ≤ m ≤ 4500). Each of the next m lines contains two integers that describe the competitors and results (the first integer a, is the winner) of a single round of competition: a and b.

Output. Print a single integer representing the number of cows whose ranks can be determined.

Sample input	Sample output
5 5 4 3 4 2 3 2 1 2 2 5	2

SOLUTION

transitive closure

Algorithm analysis

Declare a boolean matrix g, where for each pair a and b we set g[a][b] = true if the cow a wins b (an oriented edge from a to b). It is known that the results of the rounds are not contradictory, hence the graph is acyclic.

The rank of cow with number i can be determined if for any other cow j it is known that either cow i can beat j (possibly through some others), or cow j can beat i. That is, in the transitive closure of the graph, either g[i][j] = true or g[j][i] = true must be satisfied. Simultaneously g[i][j] and g[j][i] cannot be equal to true, since then the data will be inconsistent.

Example

For the given sample, you can set the ranks only for cows 2 and 5. Cow 2 will win over 5, but lose to everyone else. Cow 5 will lose to everyone.

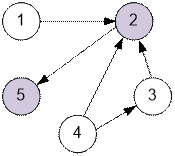
For cow 1, it is not known whether it will defeat cows 3 and 4. Accordingly, for cows 3 and 4, it is not known whether they will defeat cow 1.

Algorithm realization

Declare a boolean matrix g.

bool g[101][101];

Read the input data.

scanf("%d %d", &n, &m);

Assume that every cow wins itself.

for (i = 1; i <= n; i++) g[i][i] = 1;

Read the input data. Construct a graph.

for (i = 0; i < m; i++)

{

scanf("%d %d", &a, &b);

g[a][b] = 1;

}

Compute the transitive closure of the graph: if there is a path from vertex i to j along the edges of the graph, then set g[i][j] = true.

for (k = 1; k <= n; k++)

for (i = 1; i <= n; i++)

for (j = 1; j <= n; j++)

if (g[i][k] && g[k][j]) g[i][j] = true;

res = 0;

for (i = 1; i <= n; i++)

{

Find out is it possible to determine the rank of cow with number i. Iterate over all cows j. If for some cow g[i][j] = false and g[j][i] = false, then the result of the meeting of cows i and j is undefined and it is impossible to determine the rank of cow with number i.

bool good = true;

for (j = 1; j <= n; j++)

if (g[i][j] == false && g[j][i] == false)

{

good = false;

break;

}

If good = true, then the rank of cow number i can be set.

if (good) res++;

}

Print the answer.

printf("%d\n", res);