10157. Транзитивное замыкание

Найдите транзитивное замыкание ориентированного графа.

Вход. Ориентированный граф задан списком ребер. Первая строка содержит количество вершин n (1 ≤ n ≤ 100). Каждая из следующих строк содержит две вершины a и b (1 ≤ a, b ≤ n) описывающих ориентированное ребро от a к b.

Выход. Выведите матрицу смежности транзитивного замыкания ориентированного графа.

Пример входа	Пример выхода
4 4 1 1 2 3 4	0 1 0 0 0 0 0 0 1 1 0 1 1 1 0 0

РЕШЕНИЕ

транзитивное замыкание графа

Анализ алгоритма

В задаче следует найти транзитивное замыкание графа. Если граф содержит ребра i → k и k → j, то следует добавить ребро i → j.

Пример

Рассмотрим граф слева. Его транзитивное замыкание дано справа.

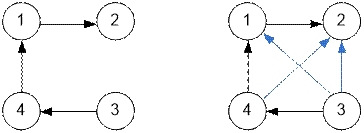
В транзитивном замыкании добавятся ребра 3 → 1 (существует путь 3 → 4 → 1), 3 → 2 (путь 3 → 4 → 1 → 2) и 4 → 2 (путь 4 → 1 → 2).

Реализация алгоритма

Объявим матрицу смежности g.

#define MAX 101

bool g[MAX][MAX];

Читаем входные данные. Строим граф.

scanf("%d", &n);

while (scanf("%d %d", &a, &b) == 2)

g[a][b] = true;

Запускаем алгоритм транзитивного замыкания. Если существуют ребра i → k и k → j, то следует провести ребро i → j.

for (k = 1; k <= n; k++)

for (i = 1; i <= n; i++)

for (j = 1; j <= n; j++)

if (g[i][k] && g[k][j]) g[i][j] = true;

Выводим матрицу смежности транзитивного замыкания графа.

for (i = 1; i <= n; i++)

{

for (j = 1; j <= n; j++)

printf("%d ", g[i][j]);

printf("\n");

}

Java реализация

import java.util.*;

public class Main

{

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

boolean g[][] = new boolean[n+1][n+1];

while (con.hasNextInt())

{

int a = con.nextInt();

int b = con.nextInt();

g[a][b] = true;

}

for (int k = 1; k <= n; k++)

for (int i = 1; i <= n; i++)

for (int j = 1; j <= n; j++)

if (g[i][k] && g[k][j]) g[i][j] = true;

for (int i = 1; i <= n; i++)

{

for (int j = 1; j <= n; j++)

{

int val = (g[i][j]) ? 1 : 0;

System.out.print(val + " ");

}

System.out.println();

}

con.close();

}

}