10157. Transitive closure
Find the transitive
closure of the directed graph.
Input. The directed graph is given with the list of edges. The first line
contains the number of vertices n (1 ≤ n ≤ 100). Each of the
next lines contains two vertices a and
b (1 ≤ a, b ≤ n) describing the directed edge
from a to b.
Output. Print the adjacency matrix of the transitive closure of the directed graph.
|
Sample input |
Sample output |
|
4 4 1 1 2 3 4 |
0 1 0 0 0 0 0 0 1 1 0 1 1 1 0 0 |
SOLUTION
transitive
closure of the graph
Algorithm analysis
In the problem you
must find the transitive closure of the graph. If
graph contains the edges i → k and k → j,
the edge i → j should be added.

Example
Consider the graph
at the left. Its transitive
closure is given at the right.
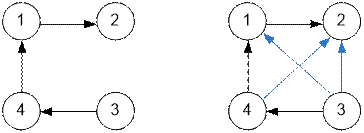
In the transitive closure the next edges will be
added: 3 → 1 (there is a
path 3 → 4 → 1), 3 → 2 (path 3 → 4 → 1 → 2) and 4 → 2 (path
4 → 1 → 2).
Algorithm
realization
Declare adjacency matrix g.
#define MAX 101
bool g[MAX][MAX];
Read the input data. Create the graph.
scanf("%d", &n);
while (scanf("%d %d", &a, &b)
== 2)
g[a][b] = true;
Start the
transitive closure algorithm. If there are edges i → k and k → j, then create an edge i → j.
for (k = 1; k <= n; k++)
for (i = 1; i <= n; i++)
for (j = 1; j <= n; j++)
if (g[i][k]
&& g[k][j]) g[i][j] = true;
Print the adjacency matrix of transitive closure of the graph.
for (i = 1; i <= n; i++)
{
for (j = 1; j
<= n; j++)
printf("%d
", g[i][j]);
printf("\n");
}
Java realization
import java.util.*;
public class Main
{
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
int n = con.nextInt();
boolean g[][] = new boolean[n+1][n+1];
while (con.hasNextInt())
{
int a = con.nextInt();
int b = con.nextInt();
g[a][b] = true;
}
for (int k = 1; k <= n; k++)
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
if (g[i][k] && g[k][j]) g[i][j] = true;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)
{
int val = (g[i][j]) ? 1 : 0;
System.out.print(val + " ");
}
System.out.println();
}
con.close();
}
}