10158. Find the centroid

Find any centroid in the tree.

Input. The first line contains one integer n (1 ≤ n ≤ 2 * 10⁵), representing the number of vertices. Each of the following n – 1 lines contains two integers v_i and u_i (1 ≤ v_i, u_i ≤ n), representing vertices connected by an edge.

It is guaranteed that the graph is a tree.

Output. Print the number of a vertex that is a centroid. If there are multiple centroids, print any one of them.

Sample input

Sample output

1 3

2 3

3 4

4 5

4 6

6 7

6 10

10 11

10 12

6 8

8 9

SOLUTION

dfs - centroid

Algorithm analysis

Consider a tree with n vertices.

A centroid of a tree is a vertex whose removal results in splitting the tree into connected components, each containing no more than n / 2 vertices. The task is to find all centroids of the tree.

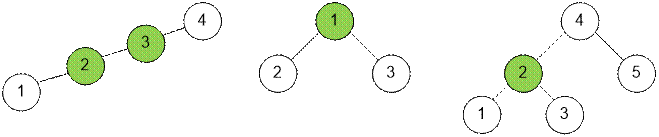
Let’s consider examples of trees and their centroids (marked in green).

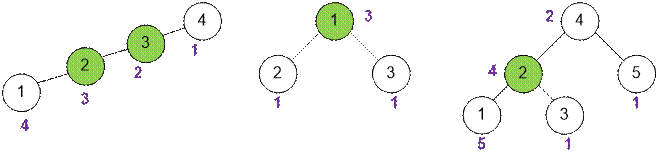
Run a depth-first search starting from vertex v, which will calculate the number of vertices in the subtree rooted at vertex v and store this value in sub[v]. For the given examples, we will indicate the corresponding value of sub[v] next to each vertex v. In all examples, the depth-first search starts from vertex 1.

If vertex v has children to₁, to₂, …, to_k , then

sub[v] = 1 + sub[to₁] + sub[to₂] + … + sub[to_k]

Vertex v is a centroid of the tree if and only if:

· for each of its children to, it holds that sub[to] ≤ n / 2;

· if we remove the subtree rooted at v from the tree, the resulting tree contains no more than n / 2 vertices: n – sub[v] ≤ n / 2;

For example, in the tree from the right with n = 5 vertices, vertex 2 is a centroid because:

· sub[4] = 2 ≤ n / 2;

· sub[3] = 1 ≤ n / 2;

· n – sub[2] = 5 – 4 = 1 ≤ n / 2;

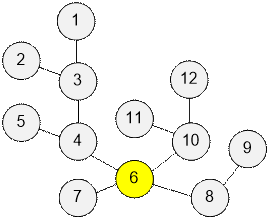
Example

Let’s consider the tree from the example. Vertex 6 is a centroid.

Algorithm realization

We’ll store the graph in the adjacency list g.

vector<vector<int> > g;

The dfs function returns the number of vertices in the subtree rooted at vertex v and saves this value in sub[v].

int dfs(int v, int p = -1)

{

sub[v] = 1;

for (int to : g[v])

if (to != p) sub[v] += dfs(to, v);

return sub[v];

}

The centroid function performs a depth-first search, finds the centroids, and stores them in the centr array.

void centroid(int v, int p = -1)

{

Set flag = 1 if vertex v is a centroid.

int flag = 1;

Iterate through the vertices to, adjacent to v. Consider an edge v → to.

for (int to : g[v])

if (to != p)

{

If for a child to it holds that sub[to] > n / 2, then v is not a centroid.

if (sub[to] > n / 2) flag = 0;

If for a child to it holds that sub[to] < n / 2, then the subtree rooted at to does not contain centroids. It makes sense to continue the search in the child to only if sub[to] ≥ n / 2.

if (sub[to] >= n / 2) centroid(to, v);

}

The tree without the subtree rooted at v contains n – sub[v] vertices. If it contains more than n / 2 vertices, then v is not a centroid.

if (n - sub[v] > n / 2) flag = 0;

If vertex v satisfies all the conditions of a centroid, add it to the centr array.

if (flag) centr.push_back(v);

}

The main part of the program. Read the input data and initialize the arrays.

scanf("%d", &n);

g.resize(n + 1);

sub.resize(n + 1);

Read the input graph.

for (i = 0; i < n - 1; i++)

{

scanf("%d %d", &a, &b);

g[a].push_back(b);

g[b].push_back(a);

}

Run a depth-first search and find the centroids of the tree.

dfs(1);

centroid(1);

Print one of the centroids.

printf("%d\n", centr[0]);

Algorithm realization – second solution

Let’s run a depth-first search dfs(v), that will compute the following values for each vertex v:

· sub[v] contains the number of vertices in the subtree with vertex v.

· f[v] contains the maximum size of a subtree among all subtrees of vertex v, including the subtree containing the parent vertex of v.

Then, the centroid will be the vertex v with the smallest value of f[v]. There may be either one or two such vertices in the tree.

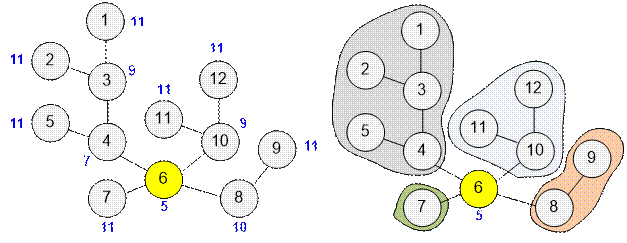
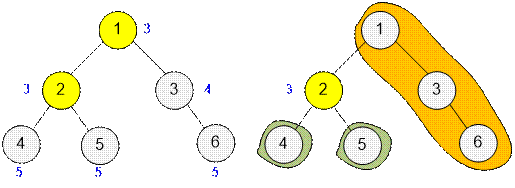
Vertex v = 6 is connected to 4 subtrees, with sizes 1, 2, 3, and 5 respectively. The value f[6] = 5 contains the maximum size of a subtree.

At the same time, the smallest value in the array f is f[6] = 5. Therefore, vertex 6 is the centroid.

Let’s consider the labeling of a tree with two centroids.

Two vertices have the smallest value in the array f: f[1] = 3 and f[2] = 3.

void dfs(int v, int p = -1)

{

sub[v] = 1;

f[v] = 0;

for (int to : g[v])

if (to != p)

{

dfs(to, v);

sub[v] += sub[to];

f[v] = max(f[v], sub[to]);

}

f[v] = max(f[v], n - sub[v]);

if ((root == 0) || (f[v] < f[root])) root = v;

}

The main part of the program. Read the input data and initialize the arrays.

scanf("%d", &n);

g.resize(n + 1);

f.resize(n + 1);

sub.resize(n + 1);

for (i = 0; i < n - 1; i++)

{

scanf("%d %d", &a, &b);

g[a].push_back(b);

g[b].push_back(a);

}

Run a depth-first search and print one of the centroids root of the tree.

root = 0;

dfs(1);

printf("%d\n", root);

Python realization

Increase the size of the stack.

import sys

sys.setrecursionlimit(300000)

The dfs function returns the number of vertices in the subtree rooted at vertex v and saves this value in sub[v].

def dfs(v, p = -1):

sub[v] = 1

for to in g[v]:

if to != p:

sub[v] += dfs(to, v)

return sub[v]

The centroid function performs a depth-first search, finds the centroids, and stores them in the centr array.

def find_centroid(v, p = -1):

Set flag = True if vertex v is a centroid.

flag = True

Iterate through the vertices to, adjacent to v. Consider an edge v → to.

for to in g[v]:

if to == p: continue

If for a child to it holds that sub[to] > n / 2, then v is not a centroid.

if sub[to] > n // 2:

flag = False

If for a child to it holds that sub[to] < n / 2, then the subtree rooted at to does not contain centroids. It makes sense to continue the search in the child to only if sub[to] ≥ n / 2.

if sub[to] >= n // 2:

find_centroid(to, v)

The tree without the subtree rooted at v contains n – sub[v] vertices. If it contains more than n / 2 vertices, then v is not a centroid.

if n - sub[v] > n // 2:

flag = False

If vertex v satisfies all the conditions of a centroid, add it to the centr array.

if flag: centr.append(v)

The main part of the program. Read the input data and initialize the arrays.

n = int(input())

g = [[] for _ in range(n + 1)]

sub = [0] * (n + 1)

centr = []

Read the input graph.

for i in range(n - 1):

a, b = map(int, input().split())

g[a].append(b)

g[b].append(a)

Run a depth-first search and find the centroids of the tree.

dfs(1)

find_centroid(1)

Print one of the centroids.

print(centr[0])

Python realization – second solution

Increase the size of the stack.

import sys

sys.setrecursionlimit(200000)

Let’s run a depth-first search dfs(v), that will compute the following values for each vertex v:

· sub[v] contains the number of vertices in the subtree with vertex v.

· f[v] contains the maximum size of a subtree among all subtrees of vertex v, including the subtree containing the parent vertex of v.

Then, the centroid will be the vertex v with the smallest value of f[v]. There may be either one or two such vertices in the tree.

def dfs(v, p=-1):

global root

sub[v] = 1

f[v] = 0

for to in g[v]:

if to != p:

dfs(to, v)

sub[v] += sub[to]

f[v] = max(f[v], sub[to])

f[v] = max(f[v], n - sub[v])

if root == 0 or f[v] < f[root]:

root = v

The main part of the program. Read the input data and initialize the arrays.

n = int(input())

g = [[] for _ in range(n + 1)]

f = [0] * (n + 1)

sub = [0] * (n + 1)

for _ in range(n - 1):

a, b = map(int, input().split())

g[a].append(b)

g[b].append(a)

Run a depth-first search and print one of the centroids root of the tree.

root = 0

dfs(1)

print(root)