10169. Ternary search
Find
the minimum of a function f(x)
= x2 + a * x + b.
Input. Two
integers a and b (|a|, |b| ≤ 106).
Output. Print the value of x where the function f(x) is minimal. Print the answer
with 2 decimal digits. It is known that |x| ≤ 100.
|
Sample input |
Sample output |
|
-2
-35 |
1.00 |
SOLUTION
ternary
search
Algorithm analysis
Let f(x) be a continuous concave function that has a local minimum on
segment [a; b]. Ternary search allows you to find the minimum point.
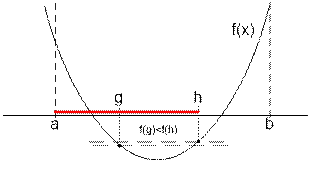
Let g = a
+ (b – a) / 3, h = a + 2 * (b – a) / 3. Points g and h divide a segment [a; b] into three equal parts (hence the
name – ternary search). Compute f(g)
and f(h).
·If f(g)
£ f(h), then the minimum point of the
function f lies on the segment [a; h], set b = h.
·If f(g)
> f(h), then the minimum point
lies on the segment [g; b], set a = g.
The search
process continues while |a – b| > e.
Example
In the sample given a function f(x) = x2 –
2 * x – 35 = (x – 7) (x + 5). Its
roots are x1 = -5, x2 = 7. The minimum of the
function is achieved at
x = (x1 + x2) / 2 = (-5 + 7) / 2 = 1
The
problem can be solved using a mathematical formula. It is known that the
minimum of the function f(x) = ax2 + bx + c (a > 0)
is achieved at x = -b /
(2a).
Therefore, the minimum of the function f(x)
= x2 + a * x + b is
achieved at x = - a / 2.
Algorithm realization
Declare the constant epsilon
ɛ = 10-7.
#define EPS 0.0000001
Declare a
function f, the minimum of which we’ll compute.
double f(double x)
{
return x * x + a * x + b;
}
Function triple finds the
minimum of the function f(x) on a segment [a; b].
double triple(double f(double x), double a, double b)
{
double g, h;
while (b - a > EPS)
{
g = a + (b - a) / 3;
h = a + 2 * (b - a) / 3;
if (f(g) <= f(h)) b = h; else a = g;
}
return (a + b) / 2;
}
The main
part of the program. Read the
input data. Start
ternary search. We are looking for the minimum of the function f(x).
scanf("%lf %lf", &a, &b);
double x = triple(f, -100, 100);
Print the value
of the minimum x.
printf("%.2lf\n", x);
Algorithm realization -a/2
#include <stdio.h>
double a, b;
int main(void)
{
scanf("%lf
%lf", &a, &b);
printf("%.2lf\n", -a/2);
return 0;
}
Java realization
import java.util.*;
public class Main
{
static final double EPS = 0.0000001;
static double a, b;
static double f(double x)
{
return x * x + a * x + b;
}
static double triple(double a, double b)
{
double g, h;
while (b - a > EPS)
{
g = a + (b - a) / 3;
h = a + 2 * (b - a) / 3;
if (f(g) <= f(h)) b = h; else a = g;
}
return (a + b) / 2;
}
public static void main(String[] args)
{
Scanner con = new
Scanner(System.in);
a = con.nextDouble();
b = con.nextDouble();
double x = triple(-100,
100);
System.out.printf("%.2f\n",x);
con.close();
}
}