10170. A * B + C
Задано натуральное число n.
Сколько существует троек (A, B, C) натуральных чисел, удовлетворяющих
равенству A * B + C = n?
Вход.
Одно натуральное число n (2 ≤ n ≤ 108).
Выход.
Выведите искомое количество троек.
|
Пример входа |
Пример выхода |
|
3 |
3 |
РЕШЕНИЕ
математика - перебор
Анализ алгоритма
Поскольку
числа A, B, C натуральные, то количество
троек, являющихся решением A * B + C = n, равно числу пар (A, B),
удовлетворяющих неравенству A * B < n. Это неравенство эквивалентно A * B ≤ n – 1, или B ≤ (n – 1) / A. Для
каждого значения А (1 ≤ А ≤ n – 1) существует
в точности ![]() таких В.
Количество искомых троек равно
таких В.
Количество искомых троек равно
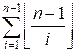
Пример
Для n = 3 имеется в точности три тройки:
·
(1, 1, 2), так
как 1 * 1 + 2 = 3;
·
(1, 2, 1), так
как 1 * 2 + 1 = 3;
·
(2, 1, 1), так
как 2 * 1 + 1 = 3.
Искомая сумма равна
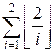 =
= 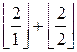 = 3
= 3
Пусть n = 7. Тогда A * B < 7 или A * B ≤ 6.
- если A = 1, то B ≤ 6 /
1 = 6. Пары (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6).
- если A = 2, то B ≤ 6 /
2 = 3. Пары (2, 1), (2, 2), (2, 3).
- если A = 3, то B ≤ 6 /
3 = 2. Пары (3, 1), (3, 2).
- если A = 4, то B ≤ 6 /
4 = 1. Пара (4, 1).
- если A = 5, то B ≤ 6 /
5 = 1. Пара (5, 1).
- если A = 6, то B ≤ 6 /
6 = 1. Пара (6, 1).
Искомая сумма равна
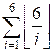 =
= 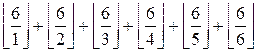 = 6 + 3 + 2 + 1 + 1 +
1 = 14
= 6 + 3 + 2 + 1 + 1 +
1 = 14
Решите задачу для n = 11.
Найдите количество троек, являющихся решением уравнения A * B + C = 11
для натуральных A, B, C.
Реализация алгоритма
Читаем
входное значение n.
scanf("%d", &n);
В
переменной res вычисляем результирующую
сумму.
res = 0;
for (i = 1; i < n; i++)
res += (n - 1) / i;
Выводим
ответ.
printf("%d\n", res);
Java реализация
import java.util.*;
public class Main
{
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
int n = con.nextInt();
int res = 0;
for (int i = 1; i < n; i++)
res += (n - 1) / i;
System.out.println(res);
con.close();
}
}
Python реализация
Читаем входное значение n.
n = int(input())
В переменной res вычисляем результирующую сумму.
res = 0;
for i in range(1, n):
res += (n - 1) // i;
Выводим ответ.
print(res)