10170. A * B + C
Positive integer n is given.
How many tuples (A, B, C) of positive integers satisfy A * B + C = n?
Input. One positive integer n (2 ≤ n ≤ 108).
Output. Print the required number of tuples.
|
Sample input |
Sample output |
|
3 |
3 |
SOLUTION
mathematics – full search
Algorithm analysis
Since the integers A,
B, C are positive, the number of triples that are the solution of A * B + C = n equals to the number of pairs (A, B)
satisfying the inequality A * B < n.
This inequality is equivalent to A * B ≤ n – 1, or B ≤ (n – 1) / A. For each value of A
(1 ≤ A ≤ n – 1), there
are exactly 
such B. The number of
triples is
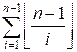
Example
For n = 3 there
are three such triples:
·
(1, 1, 2), since 1 * 1 + 2 = 3;
·
(1, 2, 1), since 1 * 2 + 1 = 3;
·
(2, 1, 1), since 2 * 1 + 1 = 3.
The required sum is
= 
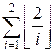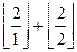= 3
Let n = 7. Then
A * B
< 7 or A * B ≤ 6.
- if A = 1, then B ≤ 6 / 1 = 6. Pairs
(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6).
- if A = 2, then B ≤ 6 / 2 = 3. Pairs
(2, 1), (2, 2), (2, 3).
- if A = 3, then B ≤ 6 / 3 = 2. Pairs
(3, 1), (3, 2).
- if A = 4, then B ≤ 6 / 4 = 1. Pair (4,
1).
- if A = 5, then B ≤ 6 / 5 = 1. Pair (5,
1).
- if A = 6, then B ≤ 6 / 6 = 1. Pair (6,
1).
The required sum is
= 
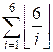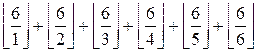= 6 + 3 + 2 + 1 + 1 +
1 = 14
Exercise
Solve the problem for n = 11. Find the number of tuples, which are solutions to the
equation A * B + C = 11
for positive integers A, B, C.
Algorithm
realization
Read the input value of n.
scanf("%d", &n);
In the variable res compute the required
sum.
res = 0;
for (i = 1; i < n; i++)
res += (n - 1) / i;
Print the answer.
printf("%d\n", res);
Java realization
import java.util.*;
public class Main
{
public static void main(String[] args)
{
Scanner
con = new Scanner(System.in);
int n = con.nextInt();
int res = 0;
for (int i = 1; i < n; i++)
res += (n - 1) / i;
System.out.println(res);
con.close();
}
}
Python realization
Read the input value of n.
n = int(input())
In the variable res compute the required
sum.
res = 0;
for i in range(1, n):
res += (n - 1) // i;
Print the answer.
print(res)