10329. Shell game
To pass the time,
Bessie the cow and her friend Elsie like to play a version of a game they saw
at the county fair.
To start, Bessie
puts three inverted shells on a table and places a small round pebble under one
of them (at least she hopes it is a pebble; she found it on the ground in one
of the pastures). Bessie then proceeds to swap pairs of shells, while Elsie
tries to guess the location of the pebble.
The standard
version of the game the cows saw being played at the county fair allowed the
player to see the initial location of the pebble, and then required guessing
its final location after all the swaps were complete.
However, the cows
like to play a version where Elsie does not know the initial location of the
pebble and can guess the pebble location after every swap. Bessie, knowing the
right answer, gives Elsie a score at the end equal to the number of correct
guesses she made.
Given the swaps
and the guesses, but not the initial pebble location, please determine the highest
possible score Elsie could have earned.
Input. The first line contains an integer n (1 ≤ n ≤ 100) giving the number of swaps. Each of the next n lines describes a step of the game and
contains three integers a, b and g, indicating that shells a and b were swapped by Bessie, and then Elsie guessed shell g after the swap was made. All three of
these integers are either 1, 2 or 3, and a ≠ b.
Output. Print the maximum number of points Elsie
could have earned.
Example. In this example, Elsie
could have earned at most 2 points. If the pebble started under
shell 1, then she is right exactly once (her final guess). If the pebble
started under shell 2, then she is right twice (the first two guesses). If
the pebble started under shell 3, then she doesn’t make any correct
guesses.
|
Sample input |
Sample output |
|
3 1 2 1 3 2 1 1 3 1 |
2 |
SOLUTION
simulation
Algorithm analysis
The pebble may initially be under the first, second,
or third shell. Let’s consider each of these three cases, and for each of them
compute the number of points that Elsie will earn. The maximum of them will be
the answer. The task reduces itself to a simulation of the game.
Example
Let’s simulate the game for three cases:
when the pebble is first under the first, the second, and the third shells. The
arrows indicate Elsie’s assumptions.
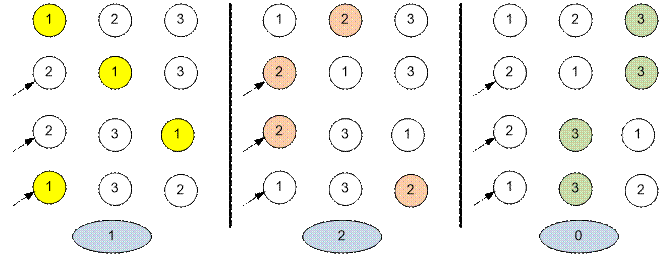
In the first case,
Elsie will guess 1 time, in the second twice, and in the third 0 times. The
maximum number of points that Elsie can earn is 2. This will be the case when
the pebble is initially under shell number 2.
Algorithm realization
The game
contains no more than 100 steps, let’s store them in arrays a, b and g.
int a[100], b[100], g[100];
Function num_correct
returns the number of points earned by Elsie provided that the pebble is
initially located under the shell number starting_shell. Initially current_shell = starting_shell.
int num_correct(int starting_shell)
{
The
variable current_shell contains the
number of the shell under which the pebble lies before each iteration.
int current_shell = starting_shell, correct = 0;
for (int i = 0; i < n; i++)
{
If the
stone is at position ai,
then it should be moved to position bi
(and vice versa).
if (a[i] == current_shell) current_shell = b[i];
else if (b[i] ==
current_shell) current_shell = a[i];
If, after
the exchange, the pebble is at position gi,
then Elsie guesses its position and earns one point.
if (current_shell == g[i]) correct++;
}
return correct;
}
The main
part of the program. Read the input data.
scanf("%d", &n);
for (i = 0; i < n; i++)
scanf("%d %d %d", &a[i], &b[i], &g[i]);
Iterate
over all the possible initial positions of the pebble: i = 1, 2, 3. For
each of them, compute the number of Elsie’s points. In the variable best
find the maximum among them.
int best = 0;
for (i = 1; i <= 3; i++)
best = max(best, num_correct(i));
Print the
answer.
printf("%d\n", best);
Algorithm realization – simulation
Store the steps of the game in arrays a, b and g.
int a[100], b[100], g[100];
Read the input data.
scanf("%d", &n);
for (i = 0; i < n; i++)
scanf("%d %d %d", &a[i],
&b[i], &g[i]);
In the variable best, compute the maximum score that Elsie can
earn.
int best = 0;
Iterate through
all the possible initial positions of the pebble: i = 1, 2, 3.
for (i = 1; i <= 3; i++)
{
The initial
position of the game is encoded in the array m. Initially, the pebble lies
under the shell i: set m[i] = 1
and set the remaining cells of the array m to zero.
int m[] = { 0, 0, 0, 0 };
m[i] = 1;
In the variable
cnt compute the number of Elsie’s correct guesses.
cnt = 0;
In the
array m simulate n steps of the game. Swap shells with numbers a[j]
and b[j]. If m[g[j]] = 1, then Elsie’s conjecture is correct.
for (j = 0; j < n; j++)
{
swap(m[a[j]], m[b[j]]);
cnt += m[g[j]];
}
Find the
maximum among all values of cnt.
if (cnt > best) best =
cnt;
}
Print the answer.
printf("%d\n", best);
Python realization – simulation
Read the number of swaps n.
n = int(input())
Store the steps of the game in arrays a, b and g.
a = [0] * n
b = [0] * n
g = [0] * n
Read the data of the game.
for i in range(n):
a[i], b[i], g[i] = map(int, input().split())
In the variable best, compute the maximum score that Elsie can
earn.
best = 0
Iterate through
all the possible initial positions of the pebble: i = 1, 2, 3.
for i in range(1, 4):
The initial
position of the game is encoded in the array m. Initially, the pebble lies
under the shell i: set m[i] = 1
and set the remaining cells of the array m to zero.
m = [0, 0, 0, 0]
m[i] = 1
In the variable
cnt compute the number of Elsie’s correct guesses.
cnt = 0
In the
array m simulate n steps of the game. Swap shells with numbers a[j]
and b[j]. If m[g[j]] = 1, then Elsie’s conjecture is correct.
for j in range(n):
m[a[j]], m[b[j]] = m[b[j]], m[a[j]]
cnt += m[g[j]]
Find the
maximum among all values of cnt.
if cnt > best:
best = cnt
Print the answer.
print(best)