10341. Сонное стадо коров (бронза)

Три лучшие коровы фермера Джона – Бесси, Элси и Милдред, всегда уходят в дальние уголки фермы! Ему нужна твоя помощь, чтобы собрать их вместе.

Главное поле на ферме длинное и узкое – его можно представить как числовую линию, на которой корова может занимать любое целое число. Три коровы в настоящее время находятся в разных целочисленных точках, и фермер Джон хочет переместить их так, чтобы они занимали три последовательные позиции (например, позиции 6, 7 и 8).

К сожалению, коровы довольно сонливы, и фермеру Джону трудно привлечь их внимание, чтобы заставить двигаться. В любой момент времени он может заставить корову двигаться, только если она является “точкой конца” (минимальной или максимальной позицией среди всех коров). Когда он перемещает корову, он может проинструктировать ее переместиться в любое незанятое целочисленное место, если только в этом новом месте она больше не является конечной точкой. Обратите внимание, что со временем эти движения сближают коров.

Определите минимальное и максимальное количество возможных ходов, прежде чем коровы сгруппируются в трех последовательных местах.

Вход. Содержит одну строку с тремя целыми числами, в которых указаны местонахождение Бесси, Элси и Милдред. Каждое местоположение представляет собой целое число в диапазоне 1 .. 10⁹.

Выход. В первой строке укажите минимальное количество ходов, которое нужно сделать фермеру Джону, чтобы сгруппировать коров вместе. Вторая строка должна содержать максимальное количество таких ходов, которые он предположительно может сделать, прежде чем коровы сгруппируются вместе.

Пример. Минимальное количество ходов 1 – если фермер Джон перемещает корову из положения 4 в положение 8, то коровы находятся в следующих друг за другом местах 7, 8, 9. Максимальное количество ходов 2. Например, корова из позиции 9 может быть перемещена в позицию 6, затем корова из позиции 7 может быть перемещена в позицию 5.

Пример входа	Пример выхода
4 7 9	1 2

РЕШЕНИЕ

моделирование

Анализ алгоритма

Пусть a, b, c – начальные местоположения Бесси, Элси и Милдред. Отсортируем координаты так чтобы a < b < c.

Вычислим сначала минимальное количество ходов.

· если все три коровы находятся рядом (a + 2 = c), то ответ 0.

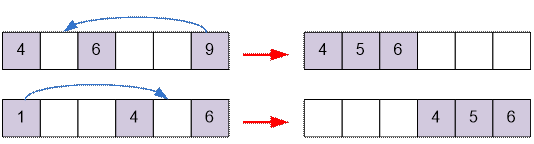
· если две коровы находятся на расстоянии 2 (a + 2 = b или b + 2 = c), то за один шаг третья корова становится между ними. Ответ 1.

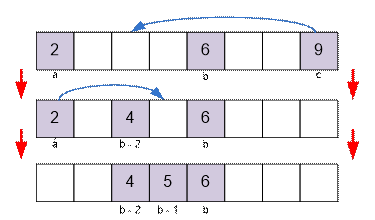
· в любом другом случае ответ 2, так как за два шага коров всегда можно поставить рядом. В этом случае расстояние между любыми двумя коровами больше 2. Например, можно корову из положения c перевести в положение b – 2, после чего корову из положения a перевести в положение b – 1.

Теперь рассмотрим как получить максимальное количество ходов. Очевидно, что за один ход либо корова a станет между b и c, либо корова c станет между a и b. Перемещение выгоднее совершать в больший интервал. То есть

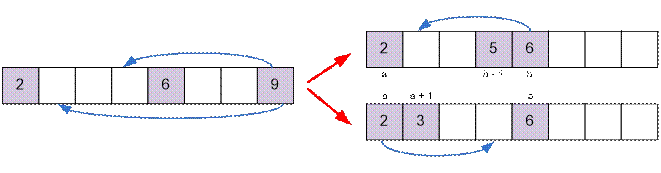
· если b – a ≥ c – b, то корову c следует поставить между a и b. Причем ставить ее можно или на позицию b – 1, или на позицию a + 1 (от этого выбора количество максимальных возможных ходов в дальнейшем не уменьшится). В первом случае в дальнейшем следует переместить корову с позиции b на a + 1. Во втором случае далее корову с позиции a следует переместить на b – 1.

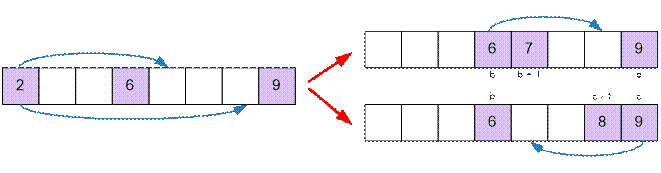
· если b – a < c – b, то корову a следует поставить между b и c. Причем ставить ее надо или на позицию b + 1, или на позицию c – 1. В первом случае в дальнейшем следует переместить корову с позиции b на c – 1. Во втором случае далее корову с позиции c следует переместить на b + 1.

Наибольшее возможное количество перемещений равно

max(b – a, c – b) – 1

Реализация алгоритма

Читаем входные данные.

scanf("%d %d %d", &a, &b, &c);

Сортируем координаты так чтобы стало a < b < c.

if (a > b) swap(a, b);

if (b > c) swap(b, c);

if (a > b) swap(a, b);

Если все три коровы находятся рядом (a + 2 = c), то ответ 0.

if (a + 2 == c) // a b c

printf("0\n");

Если две коровы находятся на расстоянии 2, то за один шаг третья корова становится между ними.

else if (a + 2 == b || b + 2 == c)

printf("1\n");

В противном случае ответ 2, так как за два шага коров всегда можно поставить рядом.

else printf("2\n");

Выводим максимальное возможное количество ходов.

printf("%d\n", max(b - a, c - b) - 1);

Java реализация

import java.util.*;

public class Main

{

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int a = con.nextInt();

int b = con.nextInt();

int c = con.nextInt();

if (a > b) a = a ^ b ^ (b = a); // swap(a, b)

if (b > c) b = b ^ c ^ (c = b); // swap(b, c)

if (a > b) a = a ^ b ^ (b = a); // swap(a, b)

if (a + 2 == c) // a b c

System.out.println(0);

else if (a + 2 == b || b + 2 == c)

System.out.println(1);

else System.out.println(2);

System.out.println(Math.max(b - a, c - b) - 1);

con.close();

}

}