10345. Покраска сарая (серебро)

Фермер Джон не умеет выполнять несколько задач одновременно. Он часто отвлекается, что затрудняет работу над долгосрочными проектами. Сейчас он пытается покрасить одну сторону своего коровника, но постоянно отвлекается на уход за коровами. В результате некоторые участки стены покрываются краской в несколько слоев, тогда как другие остаются менее окрашенными.

Сторону коровника можно представить в виде двумерной плоскости размером x × y, где фермер Джон последовательно наносит краску в виде n прямоугольных областей со сторонами, параллельными осям координат. Каждый прямоугольник задается координатами его нижнего левого и верхнего правого углов.

Фермер Джон хочет добиться равномерного покрытия стены, чтобы в ближайшее время не пришлось её перекрашивать. Однако он также не хочет тратить лишнюю краску. Оптимальным количеством слоев считается k. Ваша задача – определить площадь участка стены, который покрыт ровно k слоями краски после нанесения всех прямоугольников.

Вход. Первая строка содержит два целых числа n и k (1 ≤ k ≤ n ≤ 10⁵) – количество прямоугольников и требуемое число слоев покрытия.

Каждая из следующих n строк содержит четыре целых числа x₁, y₁, x₂, y₂, задающих прямоугольник с нижним левым углом в точке (x₁, y₁) и верхним правым углом в точке (x₂, y₂).

Все координаты x и y находятся в диапазоне от 0 до 1000. Все заданные прямоугольники имеют положительную площадь.

Выход. Выведите одно число – площадь участка стены, покрытого ровно k слоями краски.

Пример входа	Пример выхода
3 2 1 1 5 5 4 4 7 6 3 3 8 7	8

РЕШЕНИЕ

частичные суммы

Анализ алгоритма

Сначала рассмотрим одномерный вариант задачи. Пусть на числовой прямой задано n отрезков [a_i, b_i], где 0 ≤ a_i, b_i ≤ 1000. Необходимо определить, сколькими отрезками покрывается каждое целое число на этой прямой.

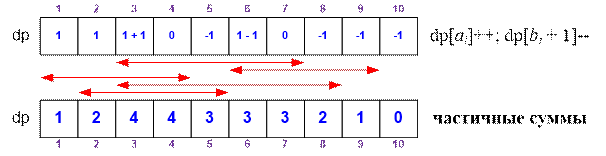
Объявим целочисленный массив dp, инициализируем его нулями. Затем для каждого отрезка [a_i, b_i] выполним две операции:

dp[a_i]++; dp[b_i + 1]-- ;

Далее вычислим префиксные суммы в массиве dp. Значение dp[i] равно количеству отрезков, содержащих число i.

Например, пусть даны следующие отрезки: [3; 7], [6; 9], [1; 4], [3; 8], [2; 5]. Инициализируем массив dp:

Для каждого отрезка [a_i, b_i] выполним две операции: dp[a_i]++; dp[b_i + 1]--.

Теперь рассмотрим двумерный вариант задачи. На плоскости задано n прямоугольников с координатами (x₁, y₁) – (x₂, y₂) (0 ≤ x₁, y₁, x₂, y₂ ≤ 1000). Требуется определить, сколькими прямоугольниками покрывается каждая клетка плоскости.

Объявим целочисленный двумерный массив dp, инициализируем его нулями. Затем для каждого прямоугольника (x₁, y₁) – (x₂, y₂) выполним четыре операции:

dp[x₁][y₁]++; dp[x₁][y₂ + 1]--; dp[x₂ + 1][y₁]--; dp[x₂ + 1][y₂ + 1]++;

После этого вычислим префиксные суммы в массиве dp. Значение dp[i][j] будет равно числу прямоугольников, содержащих клетку (i, j).

Рассмотрим, например, прямоугольник (2, 2) – (4, 5).

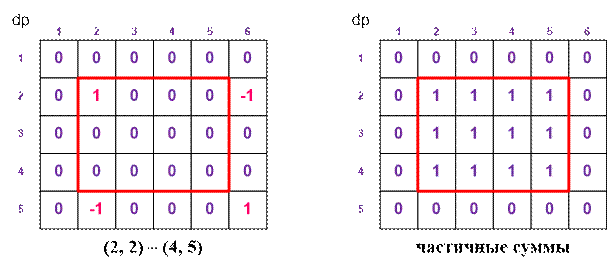
Пример

Рассмотрим приведенный пример, содержащий три прямоугольника.

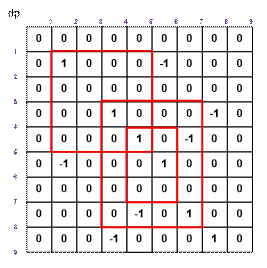
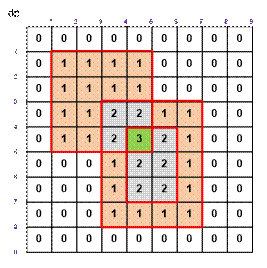
k = 2 слоями краски покрыто 8 квадратов.

Реализация алгоритма

Объявим двумерный массив dp.

#define MAX 1001

int dp[MAX][MAX];

Читаем входные данные.

scanf("%d %d", &n, &k);

while (n--)

{

Для каждого прямоугольника (a, b) – (c, d) выполним четыре операции.

scanf("%d %d %d %d", &a, &b, &c, &d);

dp[a][b]++;

dp[a][d]--;

dp[c][b]--;

dp[c][d]++;

}

В переменной res подсчитываем количество клеток стены, покрытых ровно k слоями краски.

res = 0;

Вычисляем префиксные суммы в массиве dp.

for (i = 0; i < MAX; i++)

for (j = 0; j < MAX; j++)

{

if (i) dp[i][j] += dp[i - 1][j];

if (j) dp[i][j] += dp[i][j - 1];

if (i && j) dp[i][j] -= dp[i - 1][j - 1];

Если клетка (i, j) покрыта k слоями краски, то увеличиваем res на 1,

if (dp[i][j] == k) res++;

}

Выводим ответ.

printf("%d\n", res);