10345. Painting the barn (silver)

Farmer John is not good at multitasking. He often gets distracted, which makes it difficult for him to work on long-term projects. Right now, he is trying to paint one side of his barn but constantly gets distracted by tending to his cows. As a result, some parts of the wall end up with multiple layers of paint, while others remain less covered.

The side of the barn can be represented as a two-dimensional plane of size x × y, where Farmer John sequentially applies paint in the form of n rectangular areas with sides parallel to the coordinate axes. Each rectangle is defined by the coordinates of its bottom-left and top-right corners.

Farmer John wants to achieve an even coating of the wall so that he does not have to repaint it anytime soon. However, he also does not want to waste extra paint. The optimal number of layers is considered to be k. Your task is to determine the area of the wall that is covered with exactly k layers of paint after all rectangles have been applied.

Input. The first line contains two integers n and k (1 ≤ k ≤ n ≤ 10⁵) – the number of rectangles and the required number of paint layers.

Each of the following n lines contains four integers x₁, y₁, x₂, y₂, defining a rectangle with its bottom-left corner at (x₁, y₁) and top-right corner at (x₂, y₂).

All coordinates x and y are in the range from 0 to 1000. All given rectangles have a positive area.

Output. Print one integer – the area of the wall covered with exactly k layers of paint.

Sample input	Sample output
3 2 1 1 5 5 4 4 7 6 3 3 8 7	8

SOLUTION

partial sums

Algorithm analysis

First, let’s consider the one-dimensional version of the problem. Suppose we have n segments [a_i, b_i] on a number line, where 0 ≤ a_i, b_i ≤ 1000. The goal is to determine how many segments cover each integer on this line.

We declare an integer array dp and initialize it with zeros. Then, for each segment [a_i, b_i], perform two operations:

dp[a_i]++; dp[b_i + 1]--;

Next, compute the prefix sums of the dp array. The value of dp[i] represents the number of segments that cover the number i.

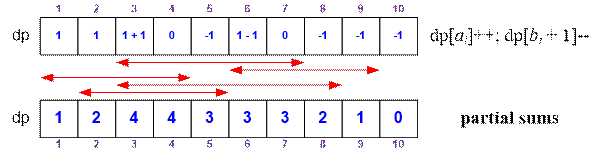
For example, consider the following set of segments: [3; 7], [6; 9], [1; 4], [3; 8], [2; 5]. Initialize the dp array:

For each segment [a_i, b_i], perform the following two operations: dp[a_i]++; dp[b_i + 1]--.

Now let’s consider the two-dimensional version of the problem. Suppose we have n rectangles on a plane, each defined by coordinates (x₁, y₁) – (x₂, y₂) (0 ≤ x₁, y₁, x₂, y₂ ≤ 1000). The goal is to determine how many rectangles cover each cell of the plane.

Declare a two-dimensional integer array dp and initialize it with zeros. Then, for each rectangle (x₁, y₁) – (x₂, y₂), perform the following four operations:

dp[x₁][y₁]++; dp[x₁][y₂ + 1]--; dp[x₂ + 1][y₁]--; dp[x₂ + 1][y₂ + 1]++;

After that, compute the prefix sums in the dp array. The value of dp[i][j] represents the number of rectangles that contain the cell (i, j).

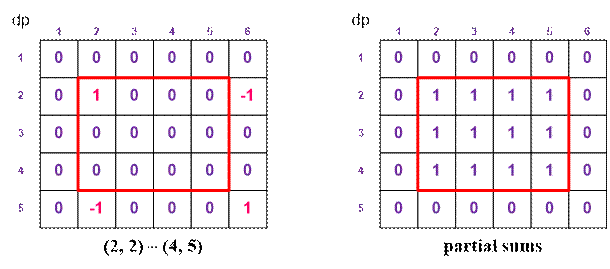
For example, consider the rectangle (2, 2) – (4, 5).

Example

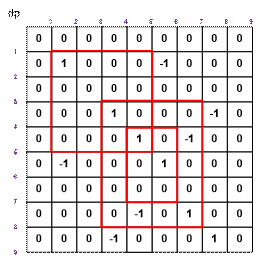
Let’s consider the given example containing three rectangles.

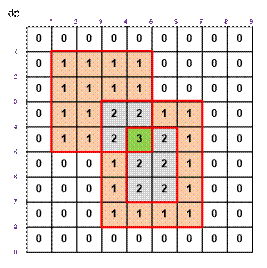
8 squares are covered with exactly 2 layers of paint.

Algorithm implementation

Declare a two-dimensional array dp.

#define MAX 1001

int dp[MAX][MAX];

Read the input data.

scanf("%d %d", &n, &k);

while (n--)

{

For each rectangle (a, b) – (c, d), perform the following four operations.

scanf("%d %d %d %d", &a, &b, &c, &d);

dp[a][b]++;

dp[a][d]--;

dp[c][b]--;

dp[c][d]++;

}

Count the number of wall cells covered with exactly k layers of paint in the variable res.

res = 0;

Compute the prefix sums in the dp array.

for (i = 0; i < MAX; i++)

for (j = 0; j < MAX; j++)

{

if (i) dp[i][j] += dp[i - 1][j];

if (j) dp[i][j] += dp[i][j - 1];

if (i && j) dp[i][j] -= dp[i - 1][j - 1];

If the cell (i, j) is covered with k layers of paint, increment res by 1.

if (dp[i][j] == k) res++;

}

Print the answer.

printf("%d\n", res);