10418. Lifeguards (bronze)

Farmer John has opened a swimming pool for his cows, figuring it will help them relax and produce more milk.

To ensure safety, he hires n cows as lifeguards, each of which has a shift that covers some contiguous interval of time during the day. For simplicity, the pool is open from time t = 0 until time t = 1000 on a daily basis, so each shift can be described by two integers, giving the time when a cow starts and ends her shift. For example, a lifeguard starting at time t = 4 and ending at time t = 7 covers three units of time (note that the endpoints are “points” in time).

Unfortunately, Farmer John hired 1 more lifeguard than he has the funds to support. Given that he must fire exactly one lifeguard, what is the maximum amount of time that can still be covered by the shifts of the remaining lifeguards? An interval of time is covered if at least one lifeguard is present.

Input. The first line contains n (1 ≤ n ≤ 100). Each of the next n lines describes a lifeguard in terms of two integers in the range 0...1000, giving the starting and ending point of a lifeguard's shift. All such endpoints are distinct. Shifts of different lifeguards might overlap.

Output. Print one number, giving the maximum amount of time that can still be covered if Farmer John fires 1 lifeguard.

Sample input	Sample output
3 5 9 1 4 3 7	7

SOLUTION

full search

Algorithm analysis

Since the number of lifeguards and time ranges are small, brute force can be used. Let’s count how many lifeguards cover each unit of time. Then iterate over each lifeguard, remove him from the list, calculate the amount of time that is covered by the rest of lifeguards. And among all such times find the maximum.

Time intervals are half-open. That is, if the shift of the lifeguard is from a to b, then he is present at work in the interval [a; b) or at times from a to b – 1 inclusive.

Example

Store in cover[i] the number of lifeguards who cover the time interval i.

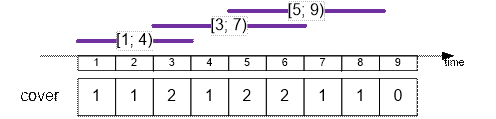
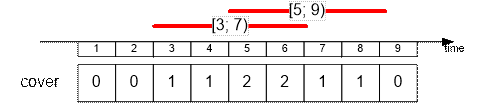
Fire the lifeguard with shift [5; 9].

The remaining lifeguards cover 6 time slots.

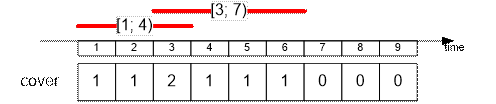
Fire the lifeguard with shift [1; 4].

The remaining lifeguards cover 6 time slots.

Fire the lifeguard with shift [3; 7].

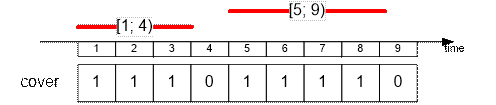
The remaining lifeguards cover 7 time slots.

It is optimal to fire the lifeguard with a shift [3; 7]. The rest of the lifeguards will be able to cover the largest number of time slots – 7.

Algorithm realization

Declare the arrays.

vector<int> start, fin, cover;

Read the input data.

scanf("%d", &n);

start.resize(n + 1);

fin.resize(n + 1);

for(i = 0; i < n; i++)

scanf("%d %d", &start[i], &fin[i]);

In the array cover count how many lifeguards cover each time interval.

cover.resize(1001);

for (i = 0; i < n; i++)

{

for (j = start[i]; j < fin[i]; j++)

cover[j]++;

}

Find the answer in the variable maxCover.

maxCover = 0;

Iterate over the lifeguards.

for (i = 0; i < n; i++)

{

Fire the lifeguard number i.

for (j = start[i]; j < fin[i]; j++)

cover[j]--;

In the variable covered count the number of intervals covered by the remaining lifeguards.

covered = 0;

for (j = 0; j < 1000; j++)

if (cover[j] > 0) covered++;

Compute the maximum among all possible values covered.

if (covered > maxCover) maxCover = covered;

Restore the lifeguard number i at the work.

for (j = start[i]; j < fin[i]; j++)

cover[j]++;

}

Print the answer.

printf("%d\n", maxCover);