10422. Мутуб
(Серебро)
В свободное время фермер Джон
создал собственную видеоплатформу под названием MooTube. На MooTube его коровы
могут записывать, публиковать и находить множество забавных видеороликов. К
настоящему моменту коровы разместили n видео с номерами от 1 до n.
Однако фермер Джон не до конца
понимает, как помочь своим коровам находить новые видео, которые им могут
понравиться. Он хочет реализовать для каждого видео систему рекомендаций – список “рекомендуемых видео”, основанный на их схожести с уже просмотренными
роликами.
Чтобы определить, насколько два
видео похожи друг на друга, Джон вводит метрику релевантности. Он вручную
оценивает n – 1 пар видео
и присваивает каждой паре значение релевантности. На основе этих пар Джон
строит сеть, где каждое видео представляет собой вершину графа, а отобранные им
пары соединяются рёбрами с указанной релевантностью.
Для удобства Джон выбирает такие n – 1 пары, чтобы между любыми двумя видео существовал
единственный путь – то есть видеосеть представляет
собой дерево.
Он решает, что релевантность
между двумя видео должна определяться как минимальная релевантность среди всех
рёбер на пути между ними.
Теперь фермер Джон хочет выбрать
значение k таким образом, чтобы для каждого видео на MooTube
отображались все другие видео, релевантность которых к нему составляет не менее
k. Однако он опасается, что слишком большое количество рекомендаций
может отвлечь коров от производства молока, поэтому ему важно точно оценить,
сколько видео будет рекомендовано для разных значений k.
Фермер Джон обращается к Вам за
помощью: нужно ответить на несколько запросов, каждый из которых содержит
значение k и номер видео. Для каждого запроса требуется определить,
сколько других видео будет рекомендовано для просмотра, если минимальная
допустимая релевантность составляет k.
Вход. Первая строка содержит два целых
числа n и q (1 ≤ n , q ≤ 5000) –
количество видеороликов и количество запросов соответственно.
Следующие n – 1 строк
описывают пары видеороликов, релевантность между которыми фермер Джон оценивает
вручную. Каждая строка содержит три целых числа pi, qi
и ri (1 ≤ pi, qi
≤ n, 1 ≤ ri ≤ 109), что означает,
что видеоролики с номерами pi и qi связаны ребром
с релевантностью ri.
Далее следуют q строк,
каждая из которых описывает один запрос от фермера Джона. В i-й строке
содержатся два целых числа ki и vi (1 ≤ ki ≤
109, 1 ≤ vi ≤ n) – это означает
что в i-ом запросе ФД интересуется, сколько видеороликов будет
рекомендовано для видео с номером vi, если минимально
допустимая релевантность рекомендаций равна k = ki.
Выход. Выведите q строк. В i
- ой строке выведите ответ на i - ый запрос ФД.
|
Пример
входа |
Пример
выхода |
|
4 3 1 2 3 2 3 2 2 4 4 1 2 4 1 3 1 |
3 0 2 |
РЕШЕНИЕ
поиск в
ширину
Анализ алгоритма
Для каждого
запроса,
заданного парой (ki, vi) запустим поиск в глубину или в ширину, начиная с вершины vi. При этом
двигаться по
графу будем только по рёбрам, релевантность которых не меньше значения ki. Подсчитаем количество
достигнутых вершин res, не считая начальную вершину vi. Значение res и будет ответом на запрос (ki, vi).
Пример
Фермер Джон установил следующие
связи между видео:
·
Видео 1 и 2 имеют релевантность 3,
·
Видео 2 и 3 – релевантность 2,
·
Видео 2 и 4 – релевантность 4.
На основании этих данных можно
вычислить релевантность между другими парами видео:
·
Видео 1 и 3: релевантность = min(3, 2) = 2,
·
Видео 1 и 4: релевантность = min(3, 4) = 3,
·
Видео 3 и 4: релевантность = min(2, 4) = 2.
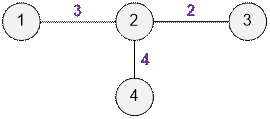
Теперь рассмотрим, какие видео
будут рекомендованы при следующих запросах:
·
Из видео 2 при k = 1 будут рекомендованы видео 1, 3 и 4.
·
Из видео 1 при k = 3 будут рекомендованы видео 2 и 4.
·
Из видео 1 при k = 4 не будет рекомендовано ни одно видео.
Реализация алгоритма – поиск в ширину
Входной
граф храним в списке смежности g.
vector<vector<pair<int, int>>> g;
Функция bfs реализует
поиск в ширину из вершины start и возвращает количество посещенных вершин, не включая саму
начальную вершину start. В процессе поиска мы переходим
только по тем ребрам, вес которых не меньше заданного значения k.
int bfs(int start, int k)
{
Массив кратчайших
расстояний в данной задаче не требуется – достаточно лишь отслеживать,
была ли вершина посещена. Если вершина i была посещена, устанавливаем
used[i] = 1.
vector<int> used(n + 1);
used[start] = 1;
Инициализируем очередь и добавляем в неё
стартовую вершину start.
queue<int> q;
q.push(start);
Количество посещенных
вершин при поиске в ширину (не считая начальную вершину start) подсчитываем в переменной res.
int res = 0;
Запускаем поиск в
ширину.
while (!q.empty())
{
Извлекаем вершину v из очереди q.
int v = q.front(); q.pop();
Перебираем ребра,
смежные с вершиной v.
for (auto edge : g[v])
{
Рассматриваем ребро (v, to) весом kto.
int to = edge.first;
int kto = edge.second;
Если вес ребра kto меньше k, то такое ребро не рассматриваем (переход
по нему запрещён).
if (kto < k) continue;
Если вершина to еще не была посещена, то добавляем ее в очередь, отмечаем как
посещённую и увеличиваем счётчик посещённых вершин res на 1.
if (used[to] == 0)
{
q.push(to);
used[to] = 1;
res++;
}
}
}
Возвращаем ответ на
запрос.
return res;
}
Основная часть
программы. Читаем входные данные.
scanf("%d %d", &n, &qu);
g.resize(n
+ 1);
for (i = 0; i < n - 1; i++)
{
scanf("%d %d %d", &p, &q, &r);
Добавляем в список
смежности неориентированное ребро (p, q) весом r.
g[p].push_back({ q, r });
g[q].push_back({ p, r });
}
Последовательно
обрабатываем qu запросов.
while (qu--)
{
scanf("%d %d", &k, &v);
Запускаем поиск в
ширину из вершины v. Выводим количество вершин, посещенных в результате поиска в
ширину.
printf("%d\n", bfs(v, k));
}
Реализация алгоритма – поиск в глубину
Входной
граф храним в списке смежности g.
vector<vector<pair<int, int>>> g;
Функция dfs выполняет
поиск в глубину, начиная с
вершины v, и
возвращает количество посещенных вершин. В процессе поиска мы перемещаемся
только по тем ребрам, у которых вес не меньше заданного значения
k.
int dfs(int v, int k)
{
Отмечаем вершину v как посещённую.
used[v] = 1;
В переменной res подсчитываем
количество вершин, посещённых в поддереве с корнем в v в ходе
выполнения поиска в глубину.
int res = 1;
Перебираем ребра,
смежные с вершиной v.
for (auto edge : g[v])
{
Рассматриваем ребро (v, to) весом kto.
int to = edge.first;
int kto = edge.second;
Если вес ребра kto меньше k, то такое ребро не рассматриваем (переход
по нему запрещён).
if (kto < k) continue;
Если вершина to еще не была посещена, то запускаем из нее поиск в глубину. Количество посещенных
вершин в поддереве с корнем to прибавляем к res.
if (used[to] == 0)
res += dfs(to, k);
}
return res;
}
Основная часть
программы. Читаем входные данные.
scanf("%d %d", &n, &qu);
g.resize(n
+ 1);
for (i = 0; i < n - 1; i++)
{
scanf("%d %d %d", &p, &q, &r);
Добавляем в список
смежности неориентированное ребро (p, q) весом r.
g[p].push_back({ q, r });
g[q].push_back({ p, r });
}
Последовательно
обрабатываем qu запросов.
while (qu--)
{
scanf("%d %d", &k, &v);
Запускаем поиск в
глубину из вершины v. Выводим количество вершин, посещенных в результате поиска в
глубину, не считая саму вершину v.
used.assign(n + 1, 0);
printf("%d\n", dfs(v, k) - 1);
}