10422_English

10422. MooTube (Silver)

In his spare time, Farmer John created his own video-sharing platform called MooTube. On MooTube, his cows can record, publish, and discover lots of funny videos. So far, the cows have uploaded n videos, numbered from 1 to n.

However, Farmer John doesn’t fully understand how to help his cows find new videos they might enjoy. He wants to implement a recommendation system for each video – a list of “recommended videos” based on their similarity to videos already watched.

To determine how similar two videos are, John introduces a relevance metric. He manually evaluates n – 1 pairs of videos and assigns each pair a relevance score. Using these pairs, John builds a network where each video is a node in a graph, and the selected pairs are connected by edges with the given relevance values.

For convenience, John selects the n – 1 pairs in such a way that there is exactly one path between any two videos – in other words, the video network forms a tree.

He decides that the relevance between two videos should be defined as the minimum relevance among all edges along the path connecting them.

Now, Farmer John wants to choose a value k such that, for any video on MooTube, all other videos with relevance at least k to it will be displayed as recommendations. However, he worries that too many recommendations might distract his cows from producing milk, so he wants to precisely estimate how many videos would be recommended for various values of k.

Farmer John turns to you for help: you are given several queries, each consisting of a value k and a video number. For each query, you need to determine how many other videos would be recommended if the minimum required relevance is k.

Input. The first line contains two integers n and q (1 ≤ n , q ≤ 5000) – the number of videos and the number of queries, respectively.

The next n – 1 lines describe pairs of videos whose relevance has been manually evaluated by Farmer John. Each of these lines contains three integers p_i, q_i and r_i (1 ≤ p_i, q_i ≤ n, 1 ≤ r_i ≤ 10⁹), meaning that videos p_i and q_i are connected by an edge with relevance r_i.

Then follow q lines, each describing one of Farmer John’s queries. The i-th line contains two integers k_i and v_i (1 ≤ k_i ≤ 10⁹, 1 ≤ v_i ≤ n) – meaning that in the i-th query, Farmer John wants to know how many videos will be recommended for video v_i if the minimum acceptable relevance for recommendations is k = k_i.

Output. Print q lines. In the i-th line, output the answer to Farmer John’s i-th query.

Sample input

Sample output

4 3

1 2 3

2 3 2

2 4 4

1 2

4 1

3 1

SOLUTION

bfs

Algorithm analysis

For each query given by the pair (k_i, v_i), perform a depth-first or breadth-first search starting from vertex v_i. During the traversal, only follow edges whose relevance is at least k_i.

Count the number of reachable vertices res, excluding the starting vertex v_i. The value of res is the answer to the query (k_i, v_i).

Example

Farmer John has established the following connections between videos:

· Video 1 and video 2 have a relevance of 3,

· Video 2 and video 3 have a relevance of 2,

· Video 2 and video 4 have a relevance of 4.

Based on this data, we can compute the relevance between other pairs of videos:

· Video 1 and video 3: relevance = min(3, 2) = 2,

· Video 1 and video 4: relevance = min(3, 4) = 3,

· Video 3 and video 4: relevance = min(2, 4) = 2.

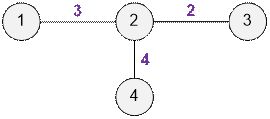
Now let’s see which videos will be recommended for the following queries:

· From video 2 with k = 1, videos 1, 3, and 4 will be recommended.

· From video 1 with k = 3, videos 2 and 4 will be recommended.

· From video 1 with k = 4, no videos will be recommended.

Algorithm implementation – breadth first search

Store the input graph in an adjacency list g.

vector<vector<pair<int, int>>> g;

The bfs function performs a breadth-first search starting from the vertex start and returns the number of visited vertices, excluding the vertex start itself. During the search, we only move along edges whose weight is at least the given value k.

int bfs(int start, int k)

{

The shortest distance array is not needed in this problem – it’s sufficient to simply track whether a vertex is visited. If vertex i is visited, set used[i] = 1.

vector<int> used(n + 1);

used[start] = 1;

Initialize a queue and add the starting vertex start to it.

queue<int> q;

q.push(start);

The number of visited vertices during the breadth-first search (excluding the starting vertex start) is counted in the variable res.

int res = 0;

Start the breadth-first search.

while (!q.empty())

{

Extract the vertex v from the queue q.

int v = q.front(); q.pop();

Iterate over all edges adjacent to vertex v.

for (auto edge : g[v])

{

Consider the edge (v, to) with weight kto.

int to = edge.first;

int kto = edge.second;

If the edge weight kto is less than k, skip this edge (moving along it is forbidden).

if (kto < k) continue;

If the vertex to is not visited yet, add it to the queue, mark it as visited, and increment the counter res by 1.

if (used[to] == 0)

{

q.push(to);

used[to] = 1;

res++;

}

Return the answer to the query.

return res;

}

The main part of the program. Read the input data.

scanf("%d %d", &n, &qu);

g.resize(n + 1);

for (i = 0; i < n - 1; i++)

{

scanf("%d %d %d", &p, &q, &r);

Add an undirected edge (p, q) with weight r to the adjacency list.

g[p].push_back({ q, r });

g[q].push_back({ p, r });

}

Process the qu queries one by one.

while (qu--)

{

scanf("%d %d", &k, &v);

Perform a breadth-first search (BFS) starting from vertex v and print the number of vertices visited during the BFS.

printf("%d\n", bfs(v, k));

}

Algorithm implementation – depth first search

Store the input graph in an adjacency list g.

vector<vector<pair<int, int>>> g;

The dfs function performs a depth-first search starting from vertex v and returns the number of visited vertices. During the search, we only traverse edges whose weight is not less than the given value k.

int dfs(int v, int k)

{

Mark vertex v as visited.

used[v] = 1;

Count the number of vertices visited in the subtree rooted at v during the depth-first search in the variable res.

int res = 1;