10452. Сочинение
В школе Азизу задали написать
сочинение. Срок сдачи приближался, а Азиз всё ещё ничего не написал. Однако он
вспомнил, что его друг Барыш в прошлом году уже выполнял это же задание, и
решил воспользоваться этим.
Азиз не хотел, чтобы система
обнаружения плагиата смогла выявить заимствование, поэтому он придумал
хитрость: переписать слова во всех предложениях сочинения Барыша в обратном
порядке. После этого Азиз решил вычислить разницу между исходным предложением и
тем, которое у него получилось.
Сочинение Барыша состоит из t
предложений. Каждое предложение включает уникальные слова. Если обозначить
количество слов в предложении числом n, то исходное предложение можно
представить как последовательность {1, 2, …, n}. Тогда предложение
Азиза будет представлено последовательностью {n, n – 1,
…, 1}.
Разница между исходным
предложением и предложением Азиза рассчитывается как сумма абсолютных значений
разниц между позициями, в которых встречается каждое слово в предложении
Барыша, и позициями, где это же слово находится в предложении Азиза.
Например, если предложение
состоит из трёх слов и предложение Барыша можно представить как {1, 2, 3}, то предложение Азиза будет {3, 2, 1}.
В этом случае разница между предложениями составит:
|1 − 3| +
|2 − 2| + |3 − 1| = 4
Вход. В первой строке задано одно
целое число t (1 ≤ t ≤ 105) – количество
предложений в сочинении Барыша. В каждой из следующих t строк
находится одно число ni (1 ≤ ni
≤ 109) – количество слов в i-ом предложении.
Выход. Для каждого предложения выведите
в отдельной строке разницу между предложениями Барыша и Азиза.
|
Пример
входа |
Пример
выхода |
|
3 4 3 7 |
8 4 24 |
РЕШЕНИЕ
математика
Анализ алгоритма
Найдем формулу для
ответа на задачу в зависимости от количества слов n в предложении.
Пусть n – четное число.
Раcсмотрим
предложения Барыша и Азиза:
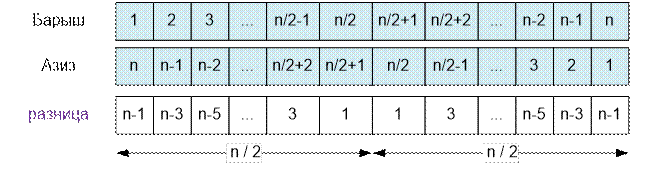
Вычислим сумму
чисел в массиве “разница”. Разобьём числа в массиве
на две равные части. Найдем сумму чисел от 1 до n – 1 с шагом 2 (это арифметическая
прогрессия). На
этом интервале имеется n / 2 чисел. Следовательно, сумма всех чисел в
массиве “разница” равна
![]() =
= ![]()
Пусть n – нечетное
число. Расcмотрим
предложения Барыша и Азиза:
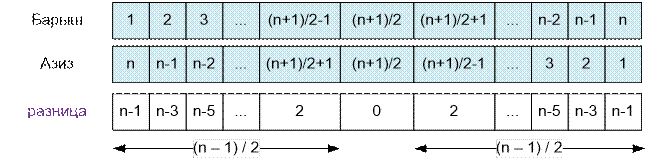
Вычислим сумму
чисел в массиве “разница”. Разобьём числа в массиве
на две равные части. Найдем сумму чисел от 2 до n – 1 с шагом 2 (это арифметическая
прогрессия). На
этом интервале имеется (n – 1) / 2 чисел. Следовательно, сумма всех чисел
в массиве “разница” равна
![]() =
= ![]() =
= ![]()
Пример
Пусть n = 8.
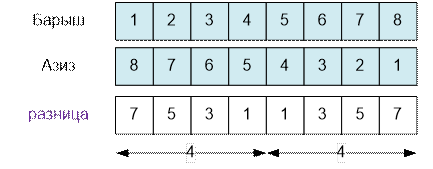
Cумма чисел в
массиве “разница” равна 82 / 2 = 32.
Пусть n = 7.
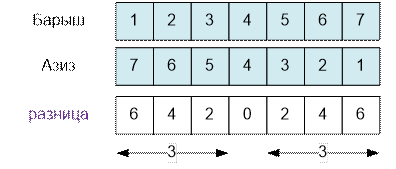
Cумма чисел в
массиве “разница” равна (72 – 1) / 2 =
24.
Реализация алгоритма
Читаем количенство тестов tests.
scanf("%d", &tests);
while (tests--)
{
Для каждого значения n вычисляем и выводим ответ.
scanf("%d", &n);
if (n
% 2 == 0)
res = n * n / 2;
else
res = (n * n - 1) / 2;
printf("%lld\n", res);
}
Python реализация
Читаем количенство тестов tests.
tests = int(input())
for _ in range(tests):
Для каждого значения n вычисляем и выводим ответ.
n = int(input())
if n % 2 == 0:
res = n * n // 2
else:
res = (n * n - 1) // 2
print(res)