10455. Linear network

A linear network consisting of n computers was installed in a big data processing center. All computers are numbered consecutively with integers from 1 to n. There is a direct connection between any two computers with consecutive numbers. Clearly, in such a network, data can be exchanged between any two computers, either directly or through intermediate ones.

However, due to the high workload, some computers may fail. In such cases, connections between certain computers are disrupted, making data transfer between them impossible.

Your task is to determine the current number of groups in the network. A group is defined as the largest subset of active computers where any two computers are connected either directly or through other computers. A group can also consist of a single computer.

You need to answer q queries. Each query either reports the failure of one of the computers or requests the current number of groups.

Input. The first line contains two integers n (1 ≤ n ≤ 10⁹) and q (1 ≤ q ≤ 10⁵) – the number of computers and the number of queries, respectively. Each of the following q lines represents a query.

Each query starts with an integer T, indicating its type. If T = 1, it is followed by an integer L (1 ≤ L ≤ n), which is the number of the computer that has failed.

· A query of type T = 1 indicates that the computer numbered L has failed.

· A query of type T = 2 requests the current number of groups in the network.

Output. For each query of the second type (T = 2), print the current number of groups in the network on a separate line.

Sample input	Sample output
4 6 1 2 2 1 4 2 1 2 2	2 2 2

SOLUTION

data structures - map

Algorithm analysis

The computers are numbered from 1 to n. Since n ≤ 10⁹, store the status of working and failed computers in a map map<int, int> m. The value of m[i] = 0 if the computer with number i is working, and m[i] = 1 if it is broken. Initially, for all 1 ≤ i ≤ n, set m[i] = 0.

For convenience, we introduce two dummy broken computers with numbers 0 and n + 1. Set m[0] = m[n + 1] = 1.

The number of groups of computers in the network will be maintained in the variable cnt. Initially, there is one group in the network, so set cnt = 1.

Now let’s consider the process of handling q queries. In particular, let’s examine the failure of the computer with number l (query type t = 1):

· If both the computer’s neighbors, on the right and left, are broken, the number of groups decreases by 1. This is because computer l, which previously represented a group of a single device, has failed.

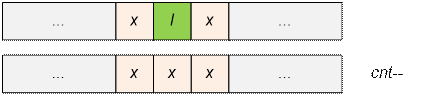
· If both the computers to the right and left of computer l are working, the number of groups will increase by 1.

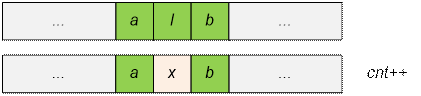
· In all other cases, the number of groups remains unchanged.

For processing a query of type t = 2, it is sufficient to print the current value of the variable cnt.

Example

Algorithm implementation

Declare a data structure map.

map<int, int> m;

Read the number of computers n and the number of queries q.

scanf("%d %d", &n, &q);

Initialize the dummy computers with numbers 0 and n + 1.

m[0] = 1;

m[n + 1] = 1;

Maintain the number of groups of computers in the network in the variable cnt. Initially, all computers are operational, so cnt = 1.

cnt = 1;

Sequentially process q queries.

while (q--)

{

scanf("%d", &t);

if (t == 1)

{

Query t = 1. The computer with number l fails. If computer l is already broken, no action is required.

scanf("%d", &l);

if (m[l] == 0)

{

Otherwise, set the state of computer l as broken.

m[l] = 1;

Depending on the state of the neighboring computers of l (either working or broken), recompute the number of groups:

· If both neighboring computers are broken, decrease cnt by 1;

· If both neighboring computers are working, increase cnt by 1;

k = m[l - 1] + m[l + 1];

if (k == 2) cnt--;

else if (k == 0) cnt++;

}

}

else

For query t = 2, print the current number of groups of computers in the network.

printf("%d\n", cnt);

}