10456. Сервер
Амин и
Мурад решили создать игровой сервер “Майнкрафт”.
На
торжественное открытие сервера они пригласили k гостей. Гости живут в
разных городах, и при подключении к серверу (в зависимости от их
местоположения) будут испытывать определённую задержку (ping). Осознав
возможные трудности, Амин и Мурад решили выбрать самое оптимальное место для
размещения сервера.
Имеется
n городов, пронумерованных от 1 до n, и m двусторонних
каналов связи между ними. Подключение к серверу возможно только по этим
каналам. С их помощью можно установить соединение между любыми двумя городами.
При этом между двумя городами может быть не более одного прямого канала связи,
а ни один город не соединён каналом сам с собой. Для каждого канала указана
задержка передачи wi.
Задержкой
соединения между каким-либо городом и сервером считается минимально возможная
сумма задержек по каналам на пути из этого города до сервера.
Амин и
Мурад хотят выбрать такой город для размещения сервера, чтобы суммарная
задержка соединений всех гостей была минимальной. Если сервер размещён в том же
городе, где живёт гость, то для него задержка считается равной нулю.
Если
существует несколько городов с одинаковой минимальной суммарной задержкой, то
Амин и Мурад выберут город с наименьшим номером.
Определите
город, в котором будет размещён сервер, и какова будет суммарная задержка
соединений всех гостей к серверу.
Вход. В первой строке заданы три
целых числа n (1 ≤ n ≤ 104), m
(1 ≤ m ≤ 4 * 104), k (1 ≤ k ≤ 100) – количество городов, количество каналов связи и
количество гостей соответственно. Во второй строке записаны k различных чисел ci (1 ≤ ci ≤
n) –
номера городов, в которых живут гости.
В каждой
из следующих m строк даны три целых числа ui, vi,
wi (1
≤ ui, vi ≤ n) –
описание двустороннего канала связи между городами ui и vi с задержкой wi
(1 ≤ wi ≤ 104).
Выход. Выведите два целых числа –
номер города, в котором будет размещён сервер, и суммарную задержку соединений
всех гостей к этому серверу.
|
Пример
входа |
Пример
выхода |
|
5 6 3 1 2 5 1 2 10 1 4 3 2 4 2 2 5 8 3 4 5 3 5 3 |
2 13 |
РЕШЕНИЕ
графы - Дейкстра
Анализ алгоритма
Поскольку n ≤ 104, для представления графа воспользуемся списком
смежности.
Запустим
алгоритм Дейкстры из всех городов, в которых проживают гости. Для каждой
вершины вычислим сумму расстояний до всех городов с гостями. Вершина с
наименьшей суммой будет оптимальным местом для размещения сервера. Если таких
вершин несколько, выбираем ту, у которой наименьший номер.
Отметим, что
сервер не обязательно должен находиться в городе, где проживает один из гостей.
Пример
Граф,
приведенный в примере, имеет следующий вид:
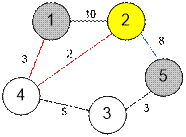
Запустим
алгоритм Дейкстры из вершин, в которых проживают гости: 1, 2 и 5. Для каждой из этих вершин определим
кратчайшие расстояния до всех остальных городов.
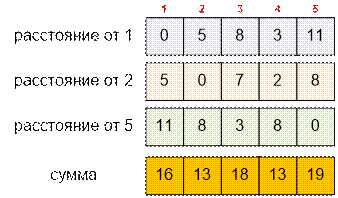
Затем для каждой
вершины графа найдём сумму расстояний до всех городов с гостями. Минимальная
сумма расстояний равна 13, и она достигается в вершине с наименьшим номером 2.
Таким образом,
сервер следует разместить в городе 2. Суммарное расстояние от него до городов,
где проживают гости, составляет 5 + 0 + 8 = 13.
Реализация алгоритма
Объявим константу
бесконечность.
#define INF 0x3F3F3F3F
Структура edge будет хранить информацию о
ребре: вершину
node, в которую ведёт ребро, и вес dist этого ребра.
struct edge
{
int node, dist;
edge(int node, int dist) : node(node), dist(dist) {}
};
Объявим компаратор для сортировки пар (node, dist) по убыванию значения dist.
bool operator< (edge a, edge b)
{
return a.dist > b.dist;
}
Объявим список смежности для представления графа.
vector<vector<edge> > g;
Функция Dijkstra реализует алгоритм Дейкстры. На вход она принимает граф g и начальную
вершину start. Возвращаемым
значением является массив d, где d[i] содержит кратчайшее расстояние от вершины start до вершины i.
void Dijkstra(vector<vector<edge> >& g, vector<int>& d, int start)
{
priority_queue<edge> pq;
pq.push(edge(start, 0));
d = vector<int>(n + 1, INF);
d[start] = 0;
while (!pq.empty())
{
edge e = pq.top();
pq.pop();
int v = e.node;
if (e.dist > d[v]) continue;
for (auto e : g[v])
{
int to = e.node;
int cost = e.dist;
if (d[v] + cost < d[to])
{
d[to] = d[v] + cost;
pq.push(edge(to, d[to]));
}
}
}
}
Основная часть программы. Читаем входные данные.
scanf("%d %d %d", &n, &m,
&k);
c.resize(k);
for (i = 0; i < k; i++)
scanf("%d", &c[i]);
Читаем входной взвешенный граф.
g.resize(n + 1);
for (i = 0; i < m; i++)
{
scanf("%d %d %d", &a, &b, &w);
g[a].push_back(edge(b, w));
g[b].push_back(edge(a, w));
}
Запускаем алгоритм Дейкстры из городов, в которых проживают
гости.
dp.resize(n + 1);
for (i = 0; i < k; i++)
{
Dijkstra(g, dist, c[i]);
for (j = 1; j <= n;
j++)
dp[j] += dist[j];
}
На данный момент dp[i] содержит сумму кратчайших расстояний от
вершины i до всех городов, в которых
находятся гости. Остаётся найти минимальное значение среди элементов массива dp
и вывести соответствующий ответ. Переменная ptr хранит наименьший номер
вершины, в которой следует разместить сервер.
res = INF;
for (i = 1; i <= n; i++)
{
if (dp[i] < res)
{
res = dp[i];
ptr = i;
}
}
Выводим ответ.
printf("%d %d\n", ptr, dp[ptr]);