10482. Подсчет
истоков
Ориентированный граф
задается списком смежности. Вершина ориентированного графа называется истоком,
если в нее не входит ни одно ребро. Подсчитайте количество истоков в графе.
Вход.
Первая строка содержит количество вершин n (1 ≤ n ≤ 100). Следующая i-ая строка содержит количество
ребер, смежных с i-ой вершиной, и номера
вершин в порядке возрастания.
Выход.
Выведите количество истоков в графе.
|
Пример входа |
Пример выхода |
|
5 1 3 2 1 3 1 5 2 1 2 2 1 2 |
1 |
РЕШЕНИЕ
графы
Анализ алгоритма
Построим матрицу
смежности графа. Далее для каждой вершины подсчитаем количество входящих в нее
ребер. Число истоков равно числу вершин, для которых количество входящих в нее
ребер равно 0.
Пример
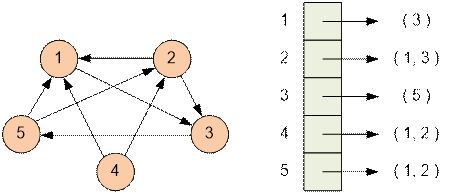
Граф содержит
один исток – вершину 4, так как в нее не входит ни одно ребро.
Реализация алгоритма
Объявим матрицу смежности и массив in, где in[i] будет содержать количество входящих в вершину i ребер.
#define MAX 101
int g[MAX][MAX], in[MAX];
Читаем входные данные. По списку смежности строим матрицу смежности.
scanf("%d", &n);
for (i = 1;
i <= n; i++)
{
Читаем количество ребер k,
смежных с вершиной
i.
scanf("%d", &k);
for (j = 0; j < k; j++)
{
Для каждого ребра (i, x) устанавливаем g[i][x] = 1.
scanf("%d", &x);
g[i][x] = 1;
}
}
Перебираем ребра графа. Для каждого ребра (i,
j) увеличиваем значение in[j] на 1 (ребро (i, j) входит
в вершину j).
for (i = 1;
i <= n; i++)
for (j = 1;
j <= n; j++)
if (g[i][j] == 1) in[j]++;
Подсчитываем количество вершин source, в
которые не входит ни одно ребро (для которых in[i] = 0).
int source
= 0;
for (i = 1;
i <= n; i++)
if (in[i] == 0) source++;
Выводим ответ.
printf("%d\n", source);