10568. Diamond collector (bronze)

Bessie the cow, always a fan of shiny objects, has taken up a hobby of mining diamonds in her spare time! She has collected n diamonds of varying sizes, and she wants to arrange some of them in a display case in the barn.

Since Bessie wants the diamonds in the case to be relatively similar in size, she decides that she will not include two diamonds in the case if their sizes differ by more than k (two diamonds can be displayed together in the case if their sizes differ by exactly k). Given k, help Bessie determine the maximum number of diamonds she can display in the case.

Input. The first line contains n (n ≤ 1000) and k (0 ≤ k ≤ 10000). The next n lines each contain an integer giving the size of one of the diamonds. All sizes will be positive and will not exceed 10000.

Output. Print the maximum number of diamonds that Bessie can showcase.

Sample input	Sample output
5 3 1 6 4 3 1	4

SOLUTION

two pointers

Algorithm analysis

Sort the array of diamond sizes. For each index i, consider the sequence m_i, m_i+1, …, m_j such that| m_j – m_i | ≤ k, but at the same time, | m_j+1 – m_i | > k. Among all such sequences, find the one that contains the largest number of elements.

Example

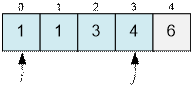
Sort the sizes of the diamonds.

Consider the interval [0; 3]. The difference between the sizes of the diamonds in this interval does not exceed k = 3. However, Bessie will not be able to showcase all the diamonds in the interval [0; 4] in the barn, since m₄ – m₀ > 3.

Algorithm realization

Declare an array to store the sizes of the diamonds.

int m[1000];

Read the input data.

scanf("%d %d", &n, &k);

for (i = 0; i < n; i++)

scanf("%d", &m[i]);

Sort the array.

sort(m, m + n);

The maximum number of diamonds that Bessie can display in the barn is counted in the variable res.

res = 0;

For each index i, consider the sequence m_i, m_i+1, …, m_j of the greatest length such that | m_j – m_i | ≤ k. Count the length of this sequence in the variable cnt.

for (i = 0; i < n; i++)

{

cnt = 0;

for (j = i; j < n; j++)

{

As soon as the condition | m_j – m_i | > k becomes true, exit the loop.

if (m[j] > m[i] + k) break;

cnt++;

}

Among the lengths of all sequences, find the maximum.

if (cnt > res) res = cnt;

}

Print the answer.

printf("%d\n", res);