10651. The smallest
topological sort
Given a directed
unweighted graph. Find its lexicographically smallest topological sorting.
Input. The first line
contains two integers n and n (1 ≤ n
≤ 105) – the number of vertices and edges in the graph. The next m lines describe the edges of the graph.
Each edge is given by a pair of integers – the starting and ending vertices.
Output. Print the
lexicographically smallest topological sorting of the graph as a sequence of
vertex numbers. If it is not possible to perform a topological sorting,
print -1.
|
Sample
input |
Sample
output |
6 61 23 24 22 56 5
4 6 |
1 3 4 2 6 5 |
SOLUTION
graphs – topological sort
Algorithm analysis
The task requires finding the
lexicographically smallest topological sort. We’ll use Kahn’s algorithm.
Instead of a classic queue, let’s use a priority queue or a set.
First, add to the queue all
vertices with no incoming edges (such vertices can start the topological sort).
In each iteration, extract the smallest element from the queue – this will
ensure that the lexicographically smallest topological sorting is constructed.
Example
The graph provided in the
example has the following structure:
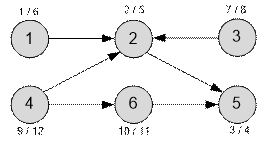
The given graph allows
multiple options for topological sorting. For example:
·
1, 4, 6, 3, 2, 5;
·
4, 3, 6, 1, 2, 5;
·
3, 1, 4, 2, 6, 5;
The lexicographically smallest
topological sort is
1, 3, 4, 2, 6, 5
The lexicographically largest topological
sort is
4, 6, 3, 1, 2, 5
Algorithm implementation – set
The input graph is stored as an
adjacency list g. The in-degrees of
the vertices are stored in the array InDegree.
The topologically sorted vertices of the graph are stored in the array Order.
vector<vector<int> > g;
vector<int> InDegree, Order;
set<int> minHeap;
Read
the input graph.
scanf("%d %d", &n,
&m);
g.resize(n + 1);
InDegree.resize(n + 1);
Calculate
the in-degrees for all vertices. For each edge (a, b) increase
the in-degree of vertex b.
for (i = 0; i < m; i++)
{
scanf("%d %d", &a, &b);
g[a].push_back(b);
InDegree[b]++;
}
All
vertices with a zero in-degree are added to the set minHeap.
for (i = 1; i < InDegree.size(); i++)
if (InDegree[i] == 0) minHeap.insert(i);
The
topological sorting algorithm continues as long as the set minHeap is not empty.
while (!minHeap.empty())
{
Extract
the vertex v with the smallest number
from minHeap and add it to the end of
the topological order.
v = *minHeap.begin();
minHeap.erase(minHeap.begin());
Order.push_back(v);
Remove
all edges (v, to) outgoing from vertex v in the
graph. For each such edge, decrease the in-degree of vertex to.
If the in-degree of vertex to becomes zero, add
it to the set, from where it will be added to the topological order list.
for (int to : g[v])
{
InDegree[to]--;
if (InDegree[to] == 0)
minHeap.insert(to);
}
}
If,
after executing the algorithm, not all n
vertices are added to the array Order, then the graph contains a cycle,
and topological sort is impossible.
if (Order.size() < n)
printf("-1");
else
Print
the vertices of the graph in the lexicographically smallest topological order.
for (i = 0; i < Order.size(); i++)
printf("%d ", Order[i]);
printf("\n");
Algorithm implementation – priority queue
#include <cstdio>
#include <queue>
#include <vector>
using namespace std;
vector<vector<int> > g;
vector<int> InDegree, Order;
priority_queue<long long, vector<long long>, greater<long long> > pq;
int i, n, m, a, b, v, to;
int main(void)
{
scanf("%d %d", &n, &m);
g.resize(n + 1);
InDegree.resize(n + 1);
for (i = 0; i < m; i++)
{
scanf("%d %d", &a, &b);
g[a].push_back(b);
InDegree[b]++;
}
for (i = 1; i <
InDegree.size(); i++)
if (InDegree[i] == 0)
pq.push(i);
while (!pq.empty())
{
v = pq.top(); pq.pop();
Order.push_back(v);
for (int to : g[v])
{
InDegree[to]--;
if (InDegree[to] == 0)
pq.push(to);
}
}
if (Order.size() < n)
printf("-1");
else
for (int x : Order)
printf("%d ", x);
printf("\n");
return 0;
}
Java implementation – priority queue
import java.util.*;
import java.io.*;
public class Main
{
static ArrayList<ArrayList<Integer>> g;
static ArrayList<Integer> top;
static int InDegree[];
static int n, m, flag = 0;
public static void main(String[] args)
{
FastScanner con = new FastScanner(System.in);
n = con.nextInt();
m = con.nextInt();
g = new
ArrayList<ArrayList<Integer>>();
InDegree = new int[n+1];
for (int i = 0; i <= n; i++)
g.add(new ArrayList<Integer>());
for (int i = 0; i < m; i++)
{
int a = con.nextInt();
int b = con.nextInt();
g.get(a).add(b);
InDegree[b]++;
}
PriorityQueue<Integer> pq = new
PriorityQueue<Integer>();
for(int i = 1; i <= n; i++)
if (InDegree[i] == 0) pq.add(i);
top = new ArrayList<Integer>();
while (!pq.isEmpty())
{
int v = pq.poll();
top.add(v);
for (int to : g.get(v))
{
InDegree[to]--;
if (InDegree[to] == 0) pq.add(to);
}
}
if (top.size() < n)
System.out.println("-1");
else
{
for (int x : top) System.out.print(x + " ");
System.out.println();
}
}
}
class FastScanner
{
BufferedReader br;
StringTokenizer st;
public FastScanner(InputStream inputStream)
{
br = new BufferedReader(new InputStreamReader(inputStream));
st = new StringTokenizer("");
}
public String next()
{
while (!st.hasMoreTokens())
{
try
{
st = new StringTokenizer(br.readLine());
} catch (Exception e)
{
return null;
}
}
return st.nextToken();
}
public int nextInt()
{
return Integer.parseInt(next());
}
}
Python implementation – priority queue
Import
the heappush and heappop functions from the heapq
module. heapq is a built-in Python library that provides an
implementation of a priority queue based on a heap.
from heapq import heappush, heappop
Read the number of vertices n
and edges m in the graph.
n, m = map(int, input().split())
The input graph is stored as an
adjacency list g. The in-degrees of
the vertices are stored in the array InDegree.
g = [[] for _ in
range(n + 1)]
InDegree = [0] * (n + 1)
Read
the input graph. Calculate the in-degrees for all vertices. For each edge (a, b)
increase the in-degree of vertex b.
for _ in range(m):
a, b = map(int, input().split())
g[a].append(b)
InDegree[b] += 1
All
vertices with a zero in-degree are added to the list minHeap.
minHeap = []
for i in range(1, len(InDegree)):
if InDegree[i] == 0:
heappush(minHeap, i)
The topologically sorted
vertices of the graph are stored in the array Order.
Order = []
The
topological sorting algorithm continues as long as the list minHeap is not empty.
while minHeap:
Extract
the vertex v with the smallest number
from minHeap and add it to the end of
the topological order.
v = heappop(minHeap)
Order.append(v)
Remove
all edges (v, to) outgoing from vertex v in the
graph. For each such edge, decrease the in-degree of vertex to.
If the in-degree of vertex to becomes zero, add
it to the priority queue, from where it will be added to the topological order
list.
for to in g[v]:
InDegree[to] -= 1
if InDegree[to] == 0:
heappush(minHeap, to)
If,
after executing the algorithm, not all n
vertices are added to the array Order, then the graph contains a cycle,
and topological sort is impossible.
if len(Order) < n:
print(-1)
Print
the vertices of the graph in the lexicographically smallest topological order.
else:
print(*Order)