10653. XOR Sum
The tree with n vertices is given. The edges of the
tree have weights of only 0 or 1.
Let’s find the XOR sum between all pairs of vertices. Compute the sum of all XOR
sums.
Input. The first line contains the number of vertices n (2 ≤ n ≤ 105) in the graph. The next n – 1 lines describe the edges.
Each line contains three integers: the numbers of the vertices connected by the
edge (vertices are numbered from 1 to n) and the weight of the edge
(0 or 1).
Output. Print the
sum of XOR sums between all pairs of vertices.
|
Sample
input |
Sample
output |
|
5 1 2 1 2 3 1 2 4 0 4 5 1 |
6 |
SOLUTION
graphs – depth first
search
Algorithm analysis
Using depth-first search,
compute the XOR sum between vertex 1 and all other vertices. Store the XOR sum
between vertex 1 and v in x[v]. Let ones be the number of ones and zeroes
be the number of zeros in the array x
(ones + zeroes = n).
Then the answer to the problem will be ones * zeroes.
Example
Consider the
graph provided in the example.
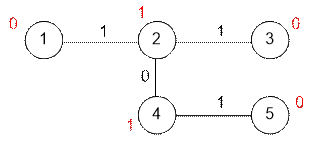
Next to each
vertex v, the XOR sum x[v] between 1 and v is written. If x[v] =
x[u] for some vertices v and u, then the XOR sum between them is equal to 0, thus contributing 0
to the total sum. The XOR sum for each pair of vertices (v, u), for which x[v] ≠ x[u], contributes 1 to the total sum.
Therefore, the
answer is equal to the number of pairs of vertices (v, u) for which x[v] ≠ x[u]. This number is equal to ones
* zeroes = 2 * 3 = 6. The pairs of
vertices that contribute 1 to the total sum are: (1, 2), (1, 4), (2, 3), (2,
5), (3, 4), (4, 5).
Algorithm implementation
Store the input graph in the
adjacency list g. Declare an array x.
vector<vector<pair<int,int> > > g;
vector<int> x;
The
dfs
function implements a depth-first search that computes the XOR sum x[v] between vertices 1 and v. The current XOR sum between 1 and v is represented by cur_xor. The parent of vertex v
is p.
void dfs(int v, int cur_xor, int p = -1)
{
x[v] = cur_xor;
for (auto z : g[v])
{
int to = z.first;
int w = z.second;
if (to != p) dfs(to, cur_xor ^ w, v);
}
}
The
main part of the program. Read the input graph.
scanf("%d", &n);
g.resize(n + 1);
x.resize(n + 1);
for (i = 1; i < n; i++)
{
scanf("%d %d %d",
&u, &v, &d);
g[u].push_back({v, d});
g[v].push_back({u, d});
}
Start
the depth-first search from vertex 1.
dfs(1, 0, -1);
Compute
the number of zeroes and ones in the array x.
ones = 0;
for (i = 1; i <= n; i++)
if (x[i] == 1) ones++;
zeroes = n - ones;
Print
the answer.
printf("%lld\n", 1LL * ones *
zeroes);
Python implementation
The
dfs
function implements a depth-first search that computes the XOR sum x[v] between vertices 1 and v. The current XOR sum between 1 and v is represented by cur_xor. The parent of vertex v
is p.
def dfs(v, cur_xor = 0, p = -1):
x[v] = cur_xor
for to, w in g[v]:
if to != p:
dfs(to, cur_xor ^ w, v)
The
main part of the program. Read the input graph.
n = int(input())
g =
[[] for _ in range(n + 1)]
for _ in range(n - 1):
u, v, d = map(int, input().split())
g[u].append((v, d))
g[v].append((u, d))
Initialize the list x.
x =
[0] * (n + 1)
Start
the depth-first search from vertex 1.
dfs(1)
Compute
the number of zeroes and ones in the list x.
ones = sum(x)
zeroes = n – ones
Print
the answer.
print(ones * zeroes)