10656. Дерево коротких расстояний
Задано
неориентированное дерево, состоящее из n
вершин. Неориентированное дерево – это связный граф с n – 1 ребром.
Ваша
задача – добавить минимальное количество ребер таким образом, чтобы длина
кратчайшего пути из вершины 1 до любой другой вершины не превышала 2. Заметьте,
что Вы не можете добавлять петли и кратные ребра.
Вход. Первая
строка содержит одно целое число n (2
≤ n ≤ 2 * 105)
– количество вершин в дереве.
Следующие
n – 1 строк описывают ребра: ребро i задано как пара вершин ui, vi (1 ≤
ui,
vi
≤ n). Гарантируется, что
заданный граф является деревом. Гарантируется, что среди заданных ребер петли и
кратные ребра отсутствуют.
Выход. Выведите
одно целое число – минимальное количество ребер, которое необходимо добавить,
чтобы длина кратчайшего пути из вершины 1 до любой другой вершины не превышает 2.
Заметьте, что вы не можете добавлять петли и кратные ребра.
|
Пример входа 1 |
Пример выхода 1 |
|
7 1 2 2 3 2 4 4 5 4 6 5 7 |
2 |
|
|
|
|
Пример входа 2 |
Пример выхода 2 |
|
7 1 2 1 3 2 4 2 5 3 6 1 7 |
0 |
РЕШЕНИЕ
графы – поиск в глубину
Анализ алгоритма
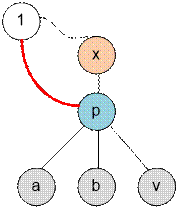
Ребра будем добавлять
из вершины 1. Действительно, если добавлено ребро (u, v), то заменив его на (1,
v), мы не ухудшим результат. Если
расстояние от 1 до вершины v больше
двух, то есть смысл провести ребро из 1 в предка v. Таким образом мы сократим до двух расстояние от вершины 1 до
всех братьев вершины v (вершины
назовем братьями если они имеют общего непосредственного предка), а также до
предка v – вершины x.
Пусть массив m содержит
вершины, расстояние до которых от вершины 1 больше 2. Вершины в массив m будем
заносить в порядке выхода из них при поиске в глубину. Далее воспользуемся
жадным подходом. Перебираем вершины из m слева направо и для каждой вершины v (если расстояние до нее еще больше
двух с учетом уже построенных ребер) проводим ребро из 1 в ее предка p. Далее все вершины, соседние с p, отмечаем таковыми, расстояние до
которых уже не больше 2.
Пример
Рассмотрим графы, приведенные в
примере.
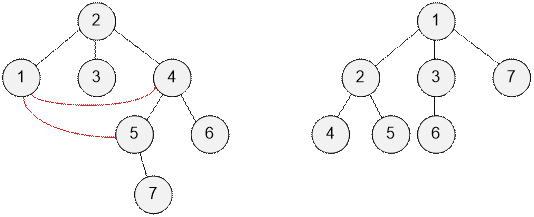
В
первом примере ответ равен 2. В массив m вершины будут занесены в порядке {7, 5,
6}. Первой на рассмотрении будет вершина v
= 7. Проводим ребро в ее предка: (1, 5). Следующей будет вершина v = 6. Проводим ребро в ее предка: (1, 4).
Во втором примере ответ 0, так
как все вершины находятся на расстоянии не более 2 от вершины 1.
Реализация алгоритма
Входной граф храним в
списке смежности g. Объявим рабочие массивы.
vector<vector<int> > g;
vector<bool> used;
vector<int> m, rev;
Функция dfs реализует поиск в глубину. Значение dist равно расстоянию от вершины 1 до v, parent – предок v.
void dfs(int v, int dist = 0, int parent = 0)
{
used[v] = true;
Для каждой вершины v сохраним
значение ее предка в rev[v].
rev[v] = parent;
for (int i = 0; i < g[v].size(); i++)
{
int to = g[v][i];
if (!used[to]) dfs(to, dist + 1, v);
}
В массиве m сохраним номера вершин дерева, расстояние до которых от 1
больше двух.
if (dist > 2) m.push_back(v);
}
Основная часть программы. Читаем входные данные.
scanf("%d", &n);
g.resize(n + 1);
for (i = 1; i < n; i++)
{
scanf("%d %d", &u, &v);
g[u].push_back(v);
g[v].push_back(u);
}
Запускаем поиск в глубину из вершины 1.
used.resize(n + 1);
rev.resize(n + 1);
dfs(1);
used.clear();
used.resize(n + 1);
В переменной ans вычисляем
результат.
int ans = 0;
Перебираем вершины, находящиеся на расстоянии больше 2 от вершины 1 (все
они находятся в массиве m). В массиве used будем отмечать вершины, расстояние
до которых от 1 уже стало равным не больше два.
for (i = 0; i <
m.size(); i++)
{
v = m[i];
if (!used[v])
{
Проводим ребро из 1 в rev[v]. Расстояние
от 1 до сыновей и предка вершины rev[v] становится не больше 2.
ans++;
used[rev[v]] = true;
for (j = 0; j < g[rev[v]].size(); j++)
{
u
= g[rev[v]][j];
used[u] = true;
}
}
}
Выводим ответ.
printf("%d\n", ans);