10656. Tree with small
distances
You are given an
undirected tree consisting of n vertices.
An undirected tree is a connected graph with n − 1 edges.
Your task is to
add the minimum number of edges in such a way that the length of the shortest path
from vertex 1 to any other vertex is at most 2. Note that you
are not allowed to add loops or multiple edges.
Input. The first line contains one integer n (2 ≤ n ≤ 2 * 105)
– the number of vertices in the tree.
The next n – 1
lines describe the edges: the i-th edge
is specified as a pair of vertices ui, vi (1 ≤ ui, vi ≤ n). It is
guaranteed that the given graph is a tree. It is guaranteed that there are no
loops or multiple edges among the given edges.
Output. Print a
single integer – the minimum number of edges that need to be added in order to
ensure that the length of the shortest path from vertex 1 to any
other vertex does not exceed 2. Note that you cannot add loops or multiple edges.
|
Sample
input 1 |
Sample
output 1 |
|
7 1 2 2 3 2 4 4 5 4 6 5 7 |
2 |
|
|
|
|
Sample
input 2 |
Sample
output 2 |
|
7 1 2 1 3 2 4 2 5 3 6 1 7 |
0 |
SOLUTION
graphs – depth first
search
Algorithm analysis
Edges will be added starting from
vertex 1. Indeed, if an edge (u, v) is added, replacing it with (1, v) will not worsen the result. If the
distance from 1 to v is greater than
two, it makes sense to draw an edge from 1 to the ancestor of v. In this way, we’ll reduce to two the
distance from 1 to all siblings
of v
(vertices are called siblings if they have a
common immediate ancestor), as well as to the ancestor of the ancestor v – the vertex x.
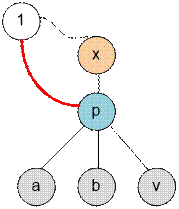
Let the array m contains the
vertices, whose distance from vertex 1 is greater than 2. The vertices in the
array m will be inserted in the order of exiting from them during the depth first
search. Next, let’s use a greedy approach. Iterate over the vertices in m from
left to right, and for each vertex v
(if the distance to it is more than 2, considering the already constructed
edges), construct an edge from 1 to its ancestor p. Then mark all vertices adjacent to p as those, the distance to which
is no more than 2.
Example
Consider the graphs shown in example.
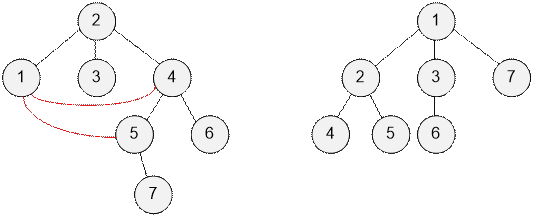
In the first
example, the answer is 2. The vertices will be stored in array m in the order
{7, 5, 6}. The first to be processed will be the vertex v = 7. We create an edge to its ancestor: (1, 5). The next for
processing will be the vertex v = 6. Create
an edge to its ancestor: (1, 4).
In the second sample, the answer is 0,
since all vertices are at a distance of no more than 2
from vertex 1.
Algorithm realization
Store the input graph in the
adjacency list g. Declare the arrays.
vector<vector<int>
> g;
vector<bool>
used;
vector<int>
m, rev;
The
dfs
function implements a depth-first search. The value of dist equals the distance from
vertex 1 to v, parent is the ancestor of v.
void dfs(int v, int dist = 0, int parent = 0)
{
used[v] = true;
For
each vertex v store the value of its
ancestor in rev[v].
rev[v] = parent;
for (int i = 0; i < g[v].size(); i++)
{
int to = g[v][i];
if (!used[to]) dfs(to, dist + 1, v);
}
In
the array m store the numbers of the tree vertices, the distance to which from
1 is more than two.
if (dist > 2) m.push_back(v);
}
The
main part of the program. Read the input data.
scanf("%d", &n);
g.resize(n + 1);
for (i = 1; i < n; i++)
{
scanf("%d %d", &u,
&v);
g[u].push_back(v);
g[v].push_back(u);
}
Run
the depth-first search from vertex 1.
used.resize(n + 1);
rev.resize(n + 1);
dfs(1);
used.clear();
used.resize(n + 1);
Compute
the result in the variable ans.
int ans = 0;
Iterate
over the vertices that are located at a distance of more
than 2 from vertex 1 (all of them are in the array m). In the used array
mark the vertices, the distance to which from 1 has already become equal to no
more than two.
for (i = 0; i < m.size(); i++)
{
v = m[i];
if
(!used[v])
{
Draw
an edge from 1 to rev[v]. The
distance from 1 to the sons of the vertex rev[v] becomes at most 2.
ans++;
used[rev[v]] = true;
for (j =
0; j < g[rev[v]].size(); j++)
{
u = g[rev[v]][j];
used[u] = true;
}
}
}
Print
the answer.
printf("%d\n",
ans);