10667. Интервалы
на дереве
Задано дерево из n вершин и n – 1 ребер, соответственно
пронумерованных 1, 2, ..., n и 1, 2,
..., n − 1. Ребро i соединяет вершины ui и vi.
Для чисел L, R (1 ≤ L ≤ R ≤ n) объявим функцию f(L, R) следующим образом:
·
Пусть S – множество вершин с номерами от L до R. Функция f (L, R) представляет собой количество
компонент связности в подграфе, образованном только из множества
вершин S и ребер,
оба конца которых принадлежат S.
Вычислите
![]()
Вход. Первая строка
содержит число n (1 ≤ n ≤ 2 * 105).
Каждая из следующих n – 1 строк содержит две вершины (ui, vi) (1 ≤ ui, vi ≤ n) – ребро в графе.
Выход. Выведите значение
суммы.
|
Пример
входа |
Пример
выхода |
|
3 1 3 2 3 |
7 |
РЕШЕНИЕ
графы –
поиск в глубину
Анализ алгоритма
Пусть V – множество вершин в
дереве, Е – множество ребер. Тогда для дерева имеет место формула:
|V| = |E| + количество компонент
связности
Тогда количество
компонент связности f(L, R) можно вычислить как |V| – |E|, где
·
V = nodes(L, R) – множество вершин
{L, …, R};
·
Е = edges(L, R) – множество ребер
с концами на множестве {L, …, R};
Искомую
сумму res = ![]() можно вычислить с помощью следующего
алгоритма:
можно вычислить с помощью следующего
алгоритма:
res = 0;
for
(L = 1; L ≤ n; L++)
for
(R = L; R ≤ n; R ++)
res
+= nodes(L, R) – edges(L, R)
Обозначим через S(n) = 1 + 2 + … + n.
Пусть L = 1. Тогда в качестве R можно выбрать вершины 1, 2, …, n.
![]() = nodes(1, 1) + nodes(1, 2) + … + nodes(1, n) =
= nodes(1, 1) + nodes(1, 2) + … + nodes(1, n) =
1 + 2 + … + n = S(n)
Пусть L = 2. Тогда в качестве R можно выбрать вершины 2, …, n.
![]() = nodes(2, 2) + nodes(2, 3) + … + nodes(2, n) =
= nodes(2, 2) + nodes(2, 3) + … + nodes(2, n) =
1 + 2 + … + n – 1 = S(n – 1)
Пусть L = k. Тогда в качестве R можно выбрать вершины k, …, n.
![]() = nodes(k,
k) + nodes(k, k + 1) + … + nodes(k, n)
=
= nodes(k,
k) + nodes(k, k + 1) + … + nodes(k, n)
=
1 + 2 + … + n – k + 1 = S(n – k + 1)
Таким образом
![]() = S(n) + S(n – 1) + … + S(1)
= S(n) + S(n – 1) + … + S(1)
Указанная сумма равна
сумме всех чисел в следующей таблице:
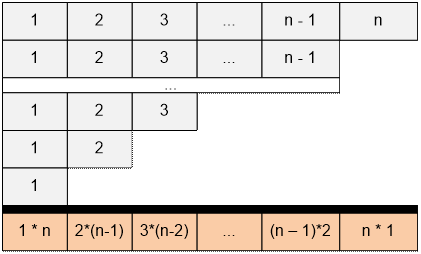
В таблице
присутствует n единиц, (n – 1) двоек, (n – 2) троек и так далее. Сумму можно переписать в виде
![]() = 1 * n + 2 * (n – 1) + 3 * (n – 2) + … + (n – 1) * 2 + n * 1
= 1 * n + 2 * (n – 1) + 3 * (n – 2) + … + (n – 1) * 2 + n * 1
Известно, что
·
![]() =
= ![]() ,
,
·
![]() =
= ![]()
Тогда
![]() =
= ![]() =
=![]() –
– ![]() =
=
![]() –
– ![]() =
= ![]() =
= ![]()
Рассмотрим ребро дерева (u, v). Оно будет входить во все множества edges(L, R), где L ≤ u и v ≤ R.
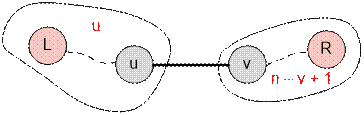
Значение L можно выбрать u способами, а значение R можно выбрать (n – v
+ 1) способами.
Следовательно количество множеств edges(L, R),
которым принадлежит ребро (u, v), равно u * (n
– v + 1).
Пример
Для приведенного примера имеются шесть возможных
пар (L, R):
·
Для L = 1, R = 1, S = {1}, имеется 1 связная компонента.
·
Для L = 1, R = 2, S = {1, 2},
имеется 2 связные
компоненты.
·
Для L = 1, R = 3, S =
{1, 2, 3}, имеется 1 связная компонента, так как S содержит оба конца каждого
из ребер 1, 2.
·
Для L = 2, R = 2, S = {2}, имеется 1 связная компонента.
·
Для L = 2, R = 3, S = {2, 3},
имеется 1 связная
компонента, так как S содержит оба конца ребра 2.
·
Для L = 3, R = 3, S = {3}, имеется 1 связная компонента.
Сумма всех значений
равна 7.
Вычислим ответ
по формуле:
![]() =
= ![]() =
= ![]() = 10
= 10
·
edges(1, 3) = 1;
·
edges(2,
3) = 2 * 1 = 2;
Следовательно
ответ равен 10 – 1 – 2 = 7.
Реализация алгоритма
Читаем входное
значение n.
scanf("%d", &n);
Инициализируем res
значением
![]() =
= ![]() .
.
res = 1LL * n * (n + 1) * (n + 2)
/ 6;
Перебираем ребра (u, v). Установим u ≤ v. Для каждого ребра
вычтем из общей суммы значение u * (n
– v + 1).
for (i = 0; i < n - 1;i++)
{
scanf("%d %d", &u, &v);
if (u > v)
{
temp = u; u = v; v = temp;
}
res -= 1LL * u * (n - v + 1);
}
Выводим ответ.
printf("%lld\n", res);