10667. Intervals on tree

We have a tree with n vertices and n – 1 edges, respectively numbered 1, 2, ..., n and 1, 2, ..., n − 1. Edge i connects vertices u_i and v_i.

For integers L, R (1 ≤ L ≤ R ≤ n), let us define a function f(L, R) as follows:

· Let S be the set of the vertices numbered L through R. f(L, R) represents the number of connected components in the subgraph formed only from the vertex set S and the edges whose endpoints both belong to S.

Compute

Input. The first line contains number n (1 ≤ n ≤ 2 * 10⁵). Each of the next n – 1 lines contains two vertices (u_i, v_i) (1 ≤ u_i, v_i ≤ n) – an edge in the graph.

Output. Print the value of the sum.

Sample input	Sample output
3 1 3 2 3	7

SOLUTION

graphs – depth first search

Algorithm analysis

Let V be the set of vertices in the tree, E be the set of edges. Then the following formula holds for a tree:

|V| = |E| + number of connected components

Then the number of connected components f (L, R) can be calculated as |V| – |E|, where

· V = nodes(L, R) – set of vertices {L, …, R};

· Е = edges(L, R) – set of edges with endpoints in {L, …, R};

The required sum res = can be computed using the following algorithm:

res = 0;

for (L = 1; L ≤ n; L++)

for (R = L; R ≤ n; R ++)

res += nodes(L, R) – edges(L, R)

Let S(n) = 1 + 2 + … + n.

Let L = 1. Then as R we can choose the vertices 1, 2, …, n.

= nodes(1, 1) + nodes(1, 2) + … + nodes(1, n) =

1 + 2 + … + n = S(n)

Let L = 2. Then as R we can choose the vertices 2, …, n.

= nodes(2, 2) + nodes(2, 3) + … + nodes(2, n) =

1 + 2 + … + n – 1 = S(n – 1)

Let L = k. Then as R we can choose the vertices k, …, n.

= nodes(k, k) + nodes(k, k + 1) + … + nodes(k, n) =

1 + 2 + … + n – k + 1 = S(n – k + 1)

Thus

= S(n) + S(n – 1) + … + S(1)

This sum equals to the sum of all numbers in the following table:

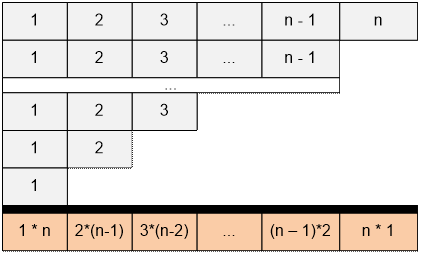
The table contains n ones, (n – 1) twos, (n – 2) triples, and so on. The sum can be rewritten as

= 1 * n + 2 * (n – 1) + 3 * (n – 2) + … + (n – 1) * 2 + n * 1

It is known that

· = ,

· =

Then

= = – =

– = =

Consider an edge of a tree (u, v). It will be included in all sets of edges (L, R), where L ≤ u and v ≤ R.

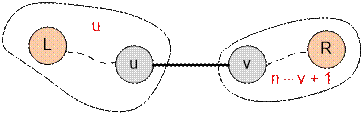
The value of L can be chosen in u ways, and the value of R can be chosen in (n – v + 1) ways. Therefore, the number of sets edges(L, R) which the edge (u, v) belongs to is u * (n – v + 1).

Example

We have six possible pairs (L, R) as follows:

· For L = 1, R = 1, S = {1} and we have 1 connected component.

· For L = 1, R = 2, S = {1, 2} and we have 2 connected components.

· For L = 1, R = 3, S = {1, 2, 3} and we have 1 connected component, since S contains both endpoints of each of the edges 1, 2.

· For L = 2, R = 2, S = {2} and we have 1 connected component.

· For L = 2, R = 3, S = {2, 3} and we have 1 connected component, since S contains both endpoints of Edge 2.

· For L = 3, R = 3, S = {3} and we have 1 connected component.

The sum of these values is 7.

Find the answer using a formula:

= = = 10

· edges(1, 3) = 1;

· edges(2, 3) = 2 * 1 = 2;

Therefore the answer is 10 – 1 – 2 = 7.

Algorithm realization

Read the value of n.

scanf("%d", &n);

Initialize res with value = .

res = 1LL * n * (n + 1) * (n + 2) / 6;

Iterate over the edges (u, v). Set u ≤ v. For each edge, subtract the value u * (n – v + 1) from the sum.

for (i = 0; i < n - 1;i++)

{

scanf("%d %d", &u, &v);

if (u > v)

{

temp = u; u = v; v = temp;

}

res -= 1LL * u * (n - v + 1);

}

Print the answer.

printf("%lld\n", res);