10668. Пути на сетке

У Вас есть лист бумаги, и Вы выбираете на нем прямоугольник размером n * m. Назовем этот прямоугольник вместе с линиями, на которых он находится, сеткой. Начиная с левого нижнего угла сетки, Вы перемещаете карандаш в правый верхний угол, следя за тем, чтобы он оставался на линиях и двигался только вправо или вверх. Результат показан слева:

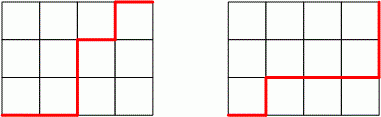
Действительно шедевр, не так ли? Повторяя процедуру еще раз, Вы получите картинку, показанную справа. Теперь возникает вопрос: сколько разных произведений искусства можно таким образом создать?

Вход. Два натуральных числа n  и m.

Выход. Выведите количество различных произведений искусства, которые можно создать, используя описанную выше процедуру. Можно утверждать, что это число соответствует 64 – битовому знаковому целому числу.

Пример входа 1	Пример выхода 1
3 4	35
Пример входа 2	Пример выхода 2
1 1	2

РЕШЕНИЕ

комбинаторика

Анализ алгоритма

Искомый путь представляет собой ломанную, состоящую из n + m звеньев. Из них n звеньев должны быть вертикальными, а остальные – горизонтальными. Количество вариантов выбрать n вертикальных звеньев из n + m равно .

Пример

Для первого примера n = 3, m = 4. Ответ равен = = = 35.

Для второго примера n = 1, m = 1. Ответ равен = = 2.

Реализация алгоритма

Функция Cnk вычисляет значение биномиального коэффициента .

long long Cnk(long long n, long long k)

{

long long res = 1;

if (k > n - k) k = n - k;

for (long long i = 1; i <= k; i++)

res = res * (n - i + 1) / i;

return res;

}

Основная часть программы. Читаем входные данные.

scanf("%lld %lld", &n, &m);

Вычисляем и выводим ответ .

res = Cnk(n + m, n);

printf("%lld\n", res);

Python реализация

import math

Читаем входные данные.

n, m = map(int,input().split())

Вычисляем и выводим ответ .

res = math.comb(n + m, n)

print(res)