10684. Roads improvement
There are n cities in the country
and n – 1 bidirectional roads, such that it is possible to travel from
any city to any other city using only these roads. The cities are numbered with
integers from 1 to n inclusive.
Initially, all roads are considered to be
in bad condition, but the government plans to improve the state of some of
them. The citizens will be satisfied with the improvements if there is no more
than one bad road on the path from the capital, located in city 1, to any other
city.
Determine the number of ways to improve the
quality of some roads to meet this requirement. Since the answer can be very
large, output it modulo 109 + 7.
Input. The first line contains a single
integer n (2 ≤ n ≤ 2 * 105)
– the number of cities
in the country. The second line contains n – 1 positive integers p2, p3, p4,
..., pn (1 ≤ pi ≤ i – 1), describing the roads in the country. The
number pi indicates that there is a road connecting city pi and city i.
Output. Print the
number of ways to improve the quality of the roads modulo 109 + 7.
|
Sample
input 1 |
Sample
output 1 |
|
3 1 1 |
4 |
|
|
|
|
Sample
input 2 |
Sample
output 2 |
|
6 1 2 2 1 5 |
15 |
SOLUTION
tree
Algorithm analysis
Let f(v) denote the number of ways
to improve the quality of roads for the subtree rooted at vertex v. Let to
represent a child of vertex v.
·
If the
road (v, to) remains in bad condition, then all roads in the
subtree rooted at vertex to must be improved.
·
If the
road (v, to) is improved, then the number of ways to improve the
roads for the subtree rooted at vertex to is equal to f(to).
Let to1, to2, …, tok be the children of v. Then
f(v) = (f(to1) + 1) * (f(to2) + 1) * … * (f(tok) + 1)
If v is a leaf (a vertex
with no children), then let f(v) = 1.
Example
Consider
the examples provided in the problem statement. For each vertex v, we’ll
record the value of f(v).
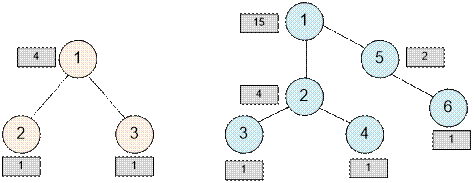
In the first example, there are 4 ways to improve the quality
of roads such that on the path from city 1 to any other city,
there is no more than one bad road. Bad roads are represented by dashed lines,
while improved roads are represented by solid lines.

Algorithm implementation
All
calculations are performed modulo MOD = 109 + 7.
#define MOD 1000000007
The dfs function computes the
value of f(v) – the number of ways to improve the quality of roads for
the subtree rooted at vertex v. The parent of v is vertex p.
long long dfs(int v, int p = -1)
{
long long s = 1;
If to1, to2, …, tok are the children of v, then
f(v) = (f(to1) + 1) * (f(to2) + 1) * … * (f(tok) + 1)
for (int to : g[v])
if (to != p)
{
long long sub = dfs(to, v);
s = (s * (sub + 1)) % MOD;
}
return s;
}
Read the input
data. Construct a tree.
scanf("%d", &n);
g.resize(n + 1);
for (i = 2; i <= n; i++)
{
scanf("%d", &p);
g[i].push_back(p);
g[p].push_back(i);
}
Compute and
print the result.
res = dfs(1);
printf("%lld\n", res);