10724. Безопасное
расстояние
Прошлый год был трудным, вирус
распространился среди населения. К счастью, Алиса знает, что один из ключей к
здоровью – держаться на безопасном расстоянии от других людей.
Алиса в настоящее время находится
в закрытой комнате, представленной в 2D-плоскости, шириной x и высотой y.
В комнате есть n человек, и нам известны их координаты (xi,
yi).
Будем рассматривать Алису и этих n
людей как точки в 2D плоскости. Начальное положение Алисы (0, 0), и она хочет
перейти к выходу в позиции (x, y). Она может свободно перемещаться
в любом направлении внутри комнаты, но не может выходить за пределы комнаты.
Найдите максимальное расстояние,
на котором Алиса может держаться от других людей при перемещении от (0, 0)
до (x, y).
Вход. Вход начинается с одной строки, содержащей
два целых числа x и y (1 ≤ x, y ≤ 106),
где x – ширина, y – высота комнаты. Вторая строка содержит
количество людей n (1 ≤ n ≤ 1000) в комнате. Каждая
из следующих n строк состоит из двух действительных чисел xi
и yi (0 ≤ xi ≤ x, 0 ≤
yi ≤ y) – координат i-го человека в
комнате.
Выход. Выведите одно действительное
число d – максимальное безопасное расстояние. Допускается аддитивная или
мультипликативная ошибка 10-5.
|
Пример
входа |
Пример
выхода |
|
8 6 3 3 1 3 5.5 6.5 1.5 |
2.250000 |
РЕШЕНИЕ
бинарный поиск
- геометрия
Анализ алгоритма
Найдем ответ на вопрос:
существует ли путь у Алисы если безопасное расстояние равно d? Если мы
ответим на этот вопрос, то наибольшее возможное d будем искать бинарным
поиском.
Представим
человека в виде круга радиуса d. Нам следует найти путь от (0, 0) до (x, y), не проходя
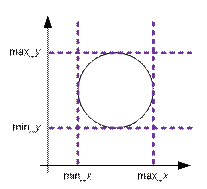
по кругам. Для каждого круга будем хранить границы его абсцисс и ординат min_x, max_x, min_y,
max_y.
Прямоугольник с противоположными вершинами (min_x, max_x) – (min_y, max_y) назовем окружающим.
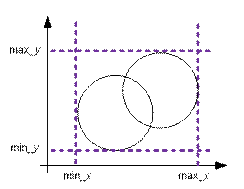
Если круги пересекаются, то будем
их объединять используя структуру непересекающихся множеств. При объединении
кругов будем пересчитывать границы абсцисс и ординат.
Рассмотрим всех
людей. Объединим все пересекающиеся круги в компоненты связности. Теперь
следует определить, существует ли путь из (0, 0) в (x, y). Для этого необходимо
выполнение следующих условий:
·
Никакой окружающий прямоугольник не содержит точку (0, 0);
·
Никакой окружающий прямоугольник не содержит точку (x, y);
·
Не существует окружающего прямоугольника, для которого min_x < 0 и max_x >
x;
·
Не существует окружающего прямоугольника, для которого min_y < 0 и max_y >
y;
Достаточно рассматривать
только те окружающие
прямоугольники, которые соответствуют кругам - представителям множеств.
Пример
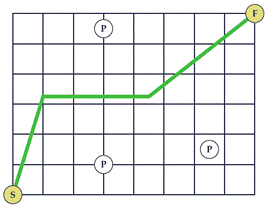
Алиса может держаться на расстоянии
2.25 от любого другого человека, и это лучшее, на что она способна. На картинке
ниже показан возможный путь.
Реализация алгоритма
Объявим константы.
const int MAX_N = 5000;
const double EPS = 1e-8;
Объявим структуру Point – точка (человек). Определим функцию Distance – евклидово расстояние между людьми. Объявим
массив точек people.
struct Point
{
double x, y;
double Distance(Point& other)
{
return sqrt((x - other.x) * (x - other.x) +
(y - other.y) * (y - other.y));
}
}
people[MAX_N + 5];
Объявим структуру кругов Circlesets. В массиве p будем поддерживать систему
непересекающихся множеств. Массив rank используется для ранговой эвристики на основе глубины деревьев.
struct CircleSets
{
double min_x[MAX_N], max_x[MAX_N], min_y[MAX_N],
max_y[MAX_N];
int p[MAX_N], rank[MAX_N];
Функция Init инициализирует данные n кругов радиуса radius. Для каждого круга вычисляем координаты противоположных вершин окружающего прямоугольника (min_x, max_x) – (min_y, max_y).
void Init(double radius)
{
for (int i = 0; i < n; ++i)
{
min_x[i] = people[i].x - radius;
max_x[i] = people[i].x + radius;
min_y[i] = people[i].y - radius;
max_y[i] = people[i].y + radius;
i-ое множество
состоит из одной i-ой вершины.
p[i] = i;
Глубина дерева с одной вершиной считается равной нулю.
rank[i] = 0;
}
}
Функция Repr возвращает
представителя множества, в котором находится элемент n. Поддерживаем
эвристику сжатия пути.
int Repr(int n)
{
if (n == p[n]) return n;
return p[n] = Repr(p[n]);
}
Функция Join объединяет
элементы i и j.
void Join(int i, int j)
{
i = Repr(i);
j = Repr(j);
if (i == j) return;
Поддерживаем
ранговую эвристику. К большему множеству присоединяем меньшее.
if (rank[i] > rank[j]) swap(i, j);
p[i] = j;
if (rank[i] == rank[j]) rank[j]++;
При объединении кругов i и j пересчитываем границы j-го окружающего прямоугольника, так как теперь он становится представителем
множества.
min_x[j] = min(min_x[j], min_x[i]);
max_x[j] = max(max_x[j], max_x[i]);
min_y[j] = min(min_y[j], min_y[i]);
max_y[j] = max(max_y[j], max_y[i]);
}
Функция HasPath проверяет,
существует ли путь из (0, 0) в (x, y).
bool HasPath()
{
for (int i = 0; i < n; i++)
{
Рассматриваем
только те круги, которые являются представителями в своих множествах.
if (p[i] != i) continue;
Проверяем
четыре условия. Если хотя бы одно из них выполняется, то путь из (0, 0) в (x, y) будет заблокирован.
if (min_x[i] < 0 && max_x[i] > x)
return false; // Horizontal
if (min_y[i] < 0 && max_y[i] > y)
return false; // Vertical
if (min_x[i] < 0 && min_y[i] < 0)
return false; // no path from
(0, 0)
if (max_x[i] > x && max_y[i] > y)
return false; // no path from
(x, y)
}
return true;
}
} circle_sets;
Функция IsSafe проверяет, является ли
безопасным путь для расстояния radius.
bool IsSafe(double radius)
{
Инициализируем множество кругов.
circle_sets.Init(radius);
Перебираем все пары кругов.
for (int i = 0; i < n; i++)
for (int j = i + 1; j < n; j++)
Если круги i и j пересекаются (расстояние между людьми i и j меньше 2 * radius), то объединяем эти
круги в одну компоненту связности.
if (people[i].Distance(people[j])
< 2 * radius)
circle_sets.Join(i, j);
return circle_sets.HasPath();
}
Функция MaxSafeDistance ищет наибольшее безопасное расстояние
между людьми, для которого существует путь у Алисы.
double MaxSafeDistance()
{
Ответ ищем бинарным поиском на отрезке [left; right] = [0; min(x,
y)].
double left = 0.0, right = min(x, y);
while (right - left > EPS)
{
double mid = (left + right) / 2;
if (IsSafe(mid)) left = mid;
else right = mid;
}
return left;
}
Основная часть программы. Читаем входные данные.
scanf("%d %d %d", &x, &y, &n);
for (i = 0; i < n; i++)
scanf("%lf %lf",
&people[i].x, &people[i].y);
Вычисляем и выводим ответ.
printf("%lf\n", MaxSafeDistance());