10725. Бег
трусцой
Фиби слышала, что физические
упражнения оказывают огромное влияние как на физическое, так и на психическое
здоровье. Она никогда раньше не бегала трусцой и хочет попробовать. Однако она
знает, что ей это быстро надоест, так как сложно многократно делать одно и то
же. Чтобы выработать привычку бегать трусцой, Фиби решила принять вызов: она
будет выходить на пробежку каждый вечер, пока находит интересный путь. Для нее
путь считается интересным, если он проходит по улице, по которой она никогда
раньше не бегала. Фиби просит Вас помочь понять, какое максимальное количество
дней она сможет выходить на пробежку, если хорошо ее спланирует.
Фиби дает Вам описание своего
района. Она живет на перекрестке и описывает все перекрестки по соседству. Она
также сообщает Вам, какие перекрестки соединены улицами, и какова длина каждой
улицы в метрах. Каждая улица соединяет два разных перекрестка. Никакие две
разные улицы не соединяют одни и те же два перекрестка. Кроме того, Вы можете
предположить, что Фиби описывает только те улицы, до которых можно добраться из
своего дома, и что улицы можно пройти в обоих направлениях, поскольку Фиби
ходит пешком.
Пробежка начинается и
заканчивается в доме Фиби, и длина пути должна быть в пределах диапазона,
указанного Фиби. Когда Фиби выходит на улицу, она не обязана проходить через
всю улицу (ей разрешено развернуться в любой точке), но даже если она это
сделает, это будет считаться, как если бы она увидела всю улицу для целей
определения интересны ли пробежки. Пробег считается интересным, если он
включает в себя улицу (или ее отрезок), которая не появлялась в предыдущих
пробежках. Достижение перекрестка не считается посещением всех прилегающих к
нему улиц.
Вход. Начинается с одной строки,
содержащей четыре целых числа I S L U. I (1 ≤ I ≤ 105)
представляет количество перекрестков в окрестности, а S (0 ≤ S ≤ 105)
представляет количество улиц. L – минимальное количество метров в допустимом
пробеге, а U (1 ≤ L ≤ U ≤ 42195, Фиби не будет бежать больше
чем марафонская дистанция) – это максимальное количество метров в допустимом
пробеге.
Затем следует S строк,
каждая из которых соответствует улице. Каждая такая строка содержит 3 целых
числа i j l. i и j – это перекрестки, которые соединяет
улица, а l – длина улицы в метрах. Перекрестки пронумерованы
от 0 до I – 1, так что Фиби живет на перекрестке с номером 0.
Выход. Выведите одно целое число, содержащее наибольшее
возможное количество интересных пробежек.
|
Пример
входа 1 |
Пример
выхода 1 |
|
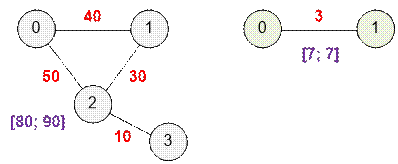
4 4 80 90 0 1 40 0 2 50 1 2 30 2 3 10 |
3 |
|
|
|
|
Пример
входа 2 |
Пример
выхода 2 |
|
2 1 7 7 0 1 3 |
1 |
РЕШЕНИЕ
графы – алгоритм
Дейкстры
Анализ алгоритма
Нижнее ограничение на длину
пробега можно не рассматривать. Если существует некоторая пробежка включающая
определенное множество улиц, то всегда можно бегать много раз по некоторому
участку одной улицы чтобы увеличить путь.
Каждую новую
пробежку следует организовывать так, чтобы на ее пути появлялась одна новая
улица. Фиби может включить в свой пробег улицу (a, b) только если расстояние
от ее дома (вершины 0) до одной из ее концов (a или b) не больше (U – 1) / 2. Деление пополам присутствует, так как Фиби должна достичь улицы и
вернуться обратно. Если вершина a достижима из 0 по
кратчайшему пути, не большем (U – 1) / 2, то в путь Фиби можно включать
любое ребро, инцидентное вершине a. Если даже, например, расстояние
от 0 до a не больше (U – 1) / 2, но расстояние от 0 до b больше (U – 1) / 2, то ребро (a, b) может быть использовано в пути Фиби:
она может добежать до вершины a, потом пройти полметра по ребру в направлении вершины b, вернуться
назад в a (пройдя также
полметра) и отправиться домой.
Таким образом наибольшее
возможное количество интересных пробежек равно числу ребер, инцидентным вершинам
графа, которые достижимы из вершины 0 на расстоянии не больше (U – 1) / 2.
Пример
Пример 1. Рассмотрим интересный 3-дневный
план пробежек:
В первый день бегаем туда-сюда по
улице между 0 и 1 (80 метров).
Во второй день пробежим 40 метров
по улице до 2, после чего вернемся тем же путем (80 метров).
На третий день бежим по улице до 1,
затем пробежим 5 метров в направлении 2, после чего вернемся назад тем же путем
(90 метров ).
Пример 2. Рассмотрим одну из возможных интересных
пробежек: бежим от 0 к 1, затем обратно к 0, потом полметра в направлении 1, и
обратно к 0.
Реализация алгоритма
Объявим следующие структуры данных:
·
g
– граф
Фиби;
·
dist – массив кратчайших расстояний от дома Фиби;
·
r_str – множество улиц, достижимых от дома Фиби на расстоянии не большем (U – 1) / 2;
vector<vector<pair<int, int>>> g;
vector<int> dist;
set<pair<int, int>> r_str; // reachable streets
Функция dijkstra реализует алгоритм Дейкстры – находит кратчайшие
расстояния в массиве dist от вершины s.
void dijkstra(int s)
{
Инициализируем кратчайшие расстояния от источника s. Положим dist[i]
= +∞, dist[s] = 0.
dist = vector<int>(g.size(), INF);
dist[s] = 0;
Очередь с приоритетами хранит пары (d, v): текущее кратчайшее расстояние до
вершины v равно d.
priority_queue<pair<int, int>, vector<pair<int, int>>,
greater<pair<int, int>>> q;
q.push({ 0, s });
Основной цикл алгоритма продолжаем пока очередь не пуста.
while (!q.empty())
{
Извлекаем из очереди вершину u с кратчайшим расстоянием d до источника.
pair<int, int> front = q.top();
q.pop();
int d = front.first, u =
front.second;
Пропускаем фиктивную вершину.
if (d > dist[u]) continue;
Перебираем ребра, исходящие из вершины u.
for (pair<int, int> next : g[u])
{
Рассматриваем ребро (u, v) весом w.
int v = next.first, w =
next.second;
Если ребро (u,
v) релаксирует, то обновляем кратчайшее расстояние dist[v].
if (dist[u] + w < dist[v])
{
dist[v] = dist[u] + w;
q.push({ dist[v], v });
}
}
}
}
Основная часть программы. Читаем входные данные. Строим граф.
scanf("%d %d %d %d", &n, &m, &junk, &U);
g.resize(n);
while (m--)
{
scanf("%d %d %d", &i, &j, &l);
g[i].push_back({ j, l });
g[j].push_back({ i, l });
}
Запускаем алгоритм Дейкстры из дома Фиби – вершины 0. Находим кратчайшие расстояния до всех вершин.
dijkstra(0);
Улицы, которые может использовать Фиби во время своих пробежек, занесем во
множество r_str. Ими являются ребра,
инцидентные вершинам на расстоянии не более (U – 1) / 2 от дома Фиби.
Перебираем вершины от 0 до n – 1.
for (u = 0; u < n; u++)
{
if (dist[u] <= (U - 1) / 2)
{
Если вершина u находится от вершины 0 на расстоянии,
не большем (U
– 1) / 2, то все ребра, инцидентные ей, заносим в r_str.
for (pair<int, int> street : g[u])
{
int v = street.first;
При этом улицы (u,
v) ориентируем так, чтобы u < v.
r_str.insert({ min(u, v), max(u, v) });
}
}
}
Количество достижимых ребер равно наибольшему возможному числу интересных пробежек.
printf("%d\n", r_str.size());